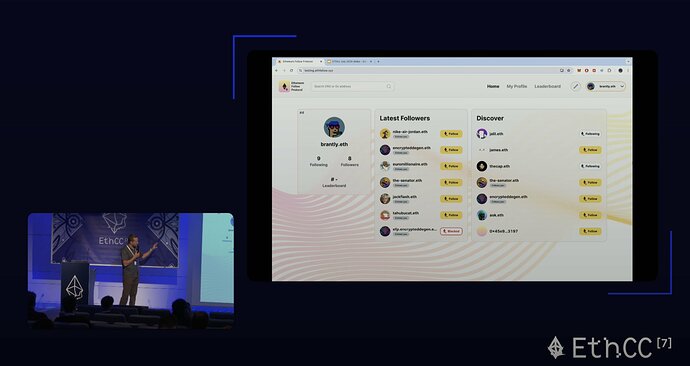
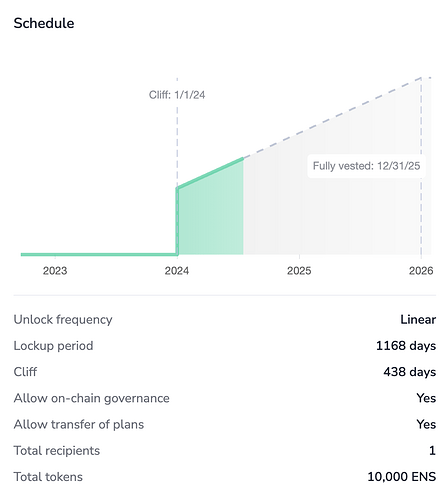
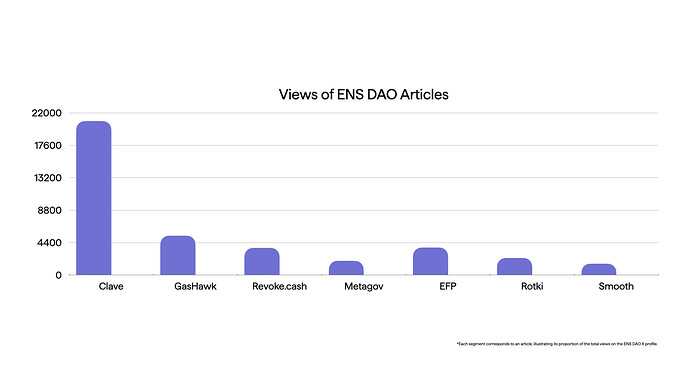
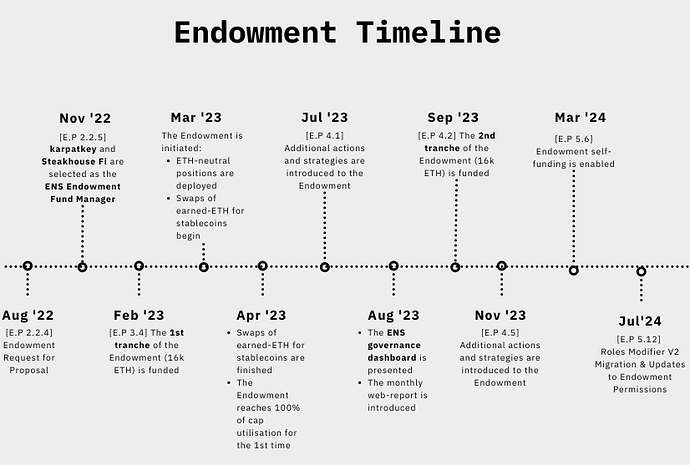
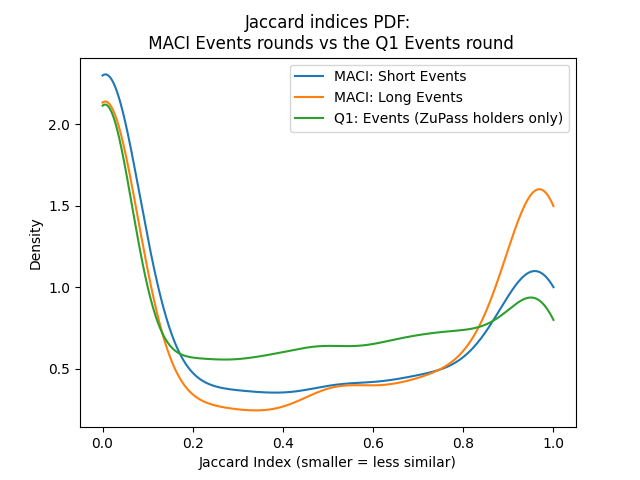
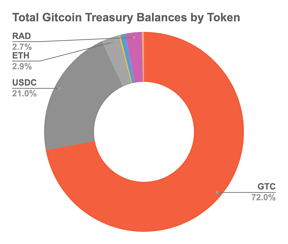
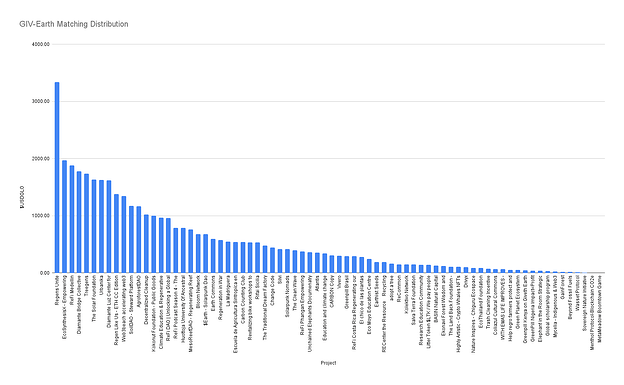
| 0x77fb4fa1aba92576942ad34bc47834059b84e693 |
890.337 |
0.2609808 |
19177.90578 |
| 0x15bf1554b8ce0a83a377b66cd5effbe3762d9166 |
638.0752 |
0.2968983 |
15635.71569 |
| 0x5648e60e7729a256f6802dcc480faed8739e629f |
530.7383 |
0.3067084 |
13435.2051 |
| 0xc6893eeb690596e44f6c8668990a5cd7b8b1cedb |
481.5 |
0.2864504 |
11383.71491 |
| 0xc0deaf6bd3f0c6574a6a625ef2f22f62a5150eab |
348.8731 |
0.3033513 |
8734.770552 |
| 0x560ddbb5ccaf91d27e91f0e7c0fa099e7ee179e6 |
290.5091 |
0.2267279 |
5436.293506 |
| 0xd68e5b216fc2af2854152eac501f9e00807d8c1d |
278.6355 |
0.3066606 |
7052.330108 |
| 0xed8db37778804a913670d9367aaf4f043aad938b |
264.1597 |
0.2733336 |
5959.335819 |
| 0x05a1ff0a32bc24265bcb39499d0c5d9a6cb2011c |
217.8 |
0.2979157 |
5355.370766 |
| 0x92ee18538c392361f1923794aa62bd3a6550c8b1 |
206.3188 |
0.3089375 |
5260.750431 |
| 0x5d28fe1e9f895464aab52287d85ebff32b351674 |
193.794 |
0.2989062 |
4780.941178 |
| 0x33878e070db7f70d2953fe0278cd32adf8104572 |
166.2382 |
0.3061801 |
4200.935484 |
| 0xd9d23db5632262033ad9f73ac8fbba8d76d00188 |
148.3895 |
0.1991725 |
2439.330899 |
| 0x1e8e749b2b578e181ca01962e9448006772b24a2 |
145.2545 |
0.2927427 |
3509.569521 |
| 0xc3176deaf906af9a7576e7407e41b24e02452fa2 |
121.6465 |
0.2501476 |
2511.506156 |
| 0x85c0c09570c955f6e07522e9ad6041716cbbb7fe |
119.4584 |
0.2908486 |
2867.621859 |
| 0x301605c95acbed7a1fd9c2c0deee964e2afbd0c3 |
119.0806 |
0.3059607 |
3007.079128 |
| 0xad9684c72fc3cc2bfc1b783249037dbb3df13459 |
107.3278 |
0.292993 |
2595.420032 |
| 0xabe46a3a4fbd37e4e0ba92a61fecd5eaa58c80ea |
102.876 |
0.2950423 |
2505.166649 |
| 0xcfc63045e2301a5ea5d105775cbcb7d5fc11ad1c |
101.4984 |
0.2701796 |
2263.340691 |
| 0x7a738effd10bf108b7617ec8e96a0722fa54c547 |
100.1174 |
0.2793339 |
2308.189343 |
| 0xb0ddea60ae36efa8c298b46ab342309fdffd66cf |
100 |
0.3068427 |
2532.526375 |
| 0xdcf37d8aa17142f053aaa7dc56025ab00d897a19 |
100 |
0.2948913 |
2433.88538 |
| 0xc0163e58648b247c143023cfb26c2baa42c9d9a9 |
100 |
0.2935752 |
2423.023643 |
| 0xc44caeb7f0724a156806664d2361fd6f32a2d2c8 |
100 |
0.2875915 |
2373.636882 |
| 0x0582f4770042113cc8a72101759e8f709c25cbe3 |
95.6649 |
0.3061259 |
2417.079253 |
| 0x79c2d72552df1c5d551b812eca906a90ce9d840a |
95.1985 |
0.2687845 |
2111.896213 |
| 0xfcf5d48463afd5ceb49e19e635f9b9ac2f8a5980 |
92.9983 |
0.1933713 |
1484.243952 |
| 0xd034fd34eaee5ec2c413c51936109e12873f4da5 |
92.0089 |
0.2946491 |
2237.552381 |
| 0xae342bc1ddace51f674151633f9fb3f52440e961 |
91.5576 |
0.2781018 |
2101.533818 |
| 0x012d5eecebadf9654b5af9b51a5b86c31ccb41c2 |
85.1386 |
0.27073 |
1902.396498 |
| 0x0a251df99a88a20a93876205fb7f5faf2e85a481 |
80.2106 |
0.2489938 |
1648.384461 |
| 0x5d00b065e722dd7cfe0695b699fb56a65f8a81cd |
77.2165 |
0.2713241 |
1729.166262 |
| 0x37c1c7347a697a174faf67a7ae5f740730e51c8e |
75.2504 |
0.2997253 |
1861.531508 |
| 0xa19a11cb5928bf07b5b6aba256f63142343a59bc |
74.6615 |
0.2531352 |
1559.866405 |
| 0xe564ef4523cb7931bafd6ecb36814b2b3691e1a4 |
74.1371 |
0.2008569 |
1229.024631 |
| 0xecfe0b6d06a645b71161f4763e1628a070bae8d6 |
71.095 |
0.3018626 |
1771.277235 |
| 0x387a161c6b25aa854100abaed39274e51aaffffd |
69 |
0.2938942 |
1673.702678 |
| 0xc2eee2987622547601d377818e527b6aee3e1048 |
68.5248 |
0.1933713 |
1093.649238 |
| 0x84e1056ed1b76fb03b43e924ef98833dba394b2b |
64.3193 |
0.2219193 |
1178.07935 |
| 0x8073639b11994c549eda58fc3cd7132a72aadf10 |
63.3129 |
0.2722961 |
1422.891885 |
| 0x79d3544bbe7821f2be4bd745d3df1f14ed211c30 |
62.28 |
0.3065238 |
1575.618093 |
| 0x71d408fba07397914cfee5ebe985e562b34fd010 |
59.3558 |
0.2870053 |
1406.019553 |
| 0x6b90e4baa3d456875620f6318fa0127388625be6 |
58.1018 |
0.2546056 |
1220.94394 |
| 0x23bc95f84bd43c1fcc2bc285fda4cb12f9aee2df |
56.9829 |
0.2579106 |
1212.975106 |
| 0x3f098c5f5e0d5b2606eed243844d1392835c1411 |
53.9243 |
0.3087423 |
1374.101704 |
| 0x1df428833f2c9fb1ef098754e5d710432450d706 |
53.77 |
0.2990172 |
1327.010903 |
| 0x28b1ea801f86accaae57cd3e32f60b8009b10269 |
52.1238 |
0.290057 |
1247.836276 |
| 0xa64f2228ccec96076c82abb903021c33859082f8 |
50.25 |
0.298517 |
1238.064624 |
| 0x83e57888cd55c3ea1cfbf0114c963564d81e318d |
50 |
0.3068427 |
1266.263189 |
| 0x92d827eeb58588bb8d3a39f3eb5077783568456a |
50 |
0.2531956 |
1044.874973 |
| 0x0fabf023b032659195f9d8590affc257412bb5d6 |
48.6032 |
0.2580632 |
1035.211635 |
| 0xa8b7522ff033d2941a0e9cecf2b32d50dfdd79c2 |
48.0588 |
0.2326592 |
922.8507366 |
| 0xd695cf5659c1c9403091f516e1232349760e2e8a |
47.7521 |
0.287908 |
1134.708763 |
| 0xf967817b892f82da16ee21fdd0667fcf9cc9caf1 |
47.5149 |
0.2263533 |
887.6767166 |
| 0xb60f993f6d7b20ffbb98e9ac8bf4b52657f8a1d5 |
44.8198 |
0.2601907 |
962.4982219 |
| 0xf3f58aaa1ec274de12a3d64a27bc571a6dd3535c |
44.4144 |
0.3071375 |
1125.887054 |
| 0x5b7575494b1e28974efe6ea71ec569b34958f72e |
42.5718 |
0.3093941 |
1087.106955 |
| 0xb9573982875b83aadc1296726e2ae77d13d9b98f |
40.9503 |
0.3087661 |
1043.577874 |
| 0xdb7a41e39807e8c988859f150296db92674b7dc7 |
40.3323 |
0.271938 |
905.2344114 |
| 0xfece25615b0bd029a638b7248a990fe23df6208d |
39.5531 |
0.1991726 |
650.2020254 |
| 0xa2e4d94c5923a8dd99c5792a7b0436474c54e1e1 |
38.2514 |
0.1991726 |
628.8036243 |
| 0x52c6eea8484707ff816864a9a1edcb0728608810 |
37.6589 |
0.305142 |
948.4354301 |
| 0x2b881a9e071172d871fd4680ba83fa293c519aab |
35.5384 |
0.3045592 |
893.3215145 |
| 0x0dbb9d306ddcd839f698adad757c95d30538603a |
35.3317 |
0.3088154 |
900.5372648 |
| 0x3fad8bcd2aea732d02a203c156b19205253f2a06 |
35 |
0.3088835 |
892.2796998 |
| 0xd4cf296a27c1af814d84c3117f13fed2ac0216da |
33.893 |
0.1933713 |
540.9290306 |
| 0x8f51dc0791cddddce08052fff939eb7cf0c17856 |
33.8749 |
0.2501741 |
699.4532011 |
| 0x2d8b0abd7980c5c9d0cb5a008a3af690c1586509 |
33.3874 |
0.2732277 |
752.9142004 |
| 0xf9e1d1e9f22c96752356adfd377231528c7e851e |
32.5413 |
0.3087898 |
829.3466569 |
| 0xab060e12d6ee092332a3a947a5714c063a206441 |
32.25 |
0.2994271 |
797.0012746 |
| 0x1ce89092d7a49fc4dcc0a7019f71b6786b318c76 |
31.6655 |
0.1945317 |
508.4110451 |
| 0x140d3f60ac840571a3e08e218b823094d4715564 |
31.6154 |
0.3004774 |
784.0589415 |
| 0x7de0e589812faa06f4018bd77de9ce8adbdded9d |
30.8866 |
0.308246 |
785.7886057 |
| 0xdcf93f31f48c691d739b6b13779a0e0d3418a6aa |
30.6029 |
0.2229813 |
563.208562 |
| 0x02d52dc45881d1f6b08d1ab9c196287624e5ffc9 |
30 |
0.3093941 |
766.0753981 |
| 0xde45f52e7998ded507b65a3112726c4a28c718bd |
29.8646 |
0.2577277 |
635.2664886 |
| 0x76963ee4c482fa4f9e125ea3c9cc2ea81fe8e8c6 |
29.6779 |
0.3058055 |
749.0601038 |
| 0x7c5cf8ed8324d3f2c972992d3fe672e4f121347d |
29.6779 |
0.2887276 |
707.228279 |
| 0xed6e5b9c3ceceebd77a58b31dccb6a93fe1d91d1 |
29.0509 |
0.3093941 |
741.8393261 |
| 0xf6eb526bffa8d5036746df58fef23fb091739c44 |
28.3714 |
0.3087898 |
723.0727037 |
| 0x2beba030cdc9c4a47c5aa657974840428b9fefac |
28.3025 |
0.3053119 |
713.1925144 |
| 0x6c35574c71390b410755af14ae08f121f0f04f62 |
28.1627 |
0.3005382 |
698.5736284 |
| 0x3ae1a0c147430ff475957472d8b4e5d3cd6c1b33 |
27.8994 |
0.3083288 |
709.9816849 |
| 0x5b655eda7d101f98934392cc3610bcb25b633789 |
27 |
0.3029596 |
675.1290112 |
| 0xb1bd3dbbe482e61d9d9f2a82f506b7cb84b6d80b |
26.8781 |
0.1991724 |
441.8410082 |
| 0x8758e5741de847363dd2715a62431cc0cbda4ca6 |
25.0281 |
0.2470896 |
510.4116 |
| 0xbc8689a07a4fa38cba728af18cc9b057248e4caf |
24.0283 |
0.271525 |
538.4819655 |
| 0xab87eb50280a340b42f4eab31db90714b39fe687 |
23.9902 |
0.3093941 |
612.6100672 |
| 0xf9ee4d476fda5c63ac7cb9e42909eb986303ccbf |
23.0826 |
0.2600845 |
495.4929296 |
| 0xa2019fecdc83c0fe37d0ed8b3bc0df6b8373602b |
22.8807 |
0.3033814 |
572.9232088 |
| 0x826976d7c600d45fb8287ca1d7c76fc8eb732030 |
22.8712 |
0.2285894 |
431.5024632 |
| 0x5255e33362f533a947ba801f4f3a813d82fa8341 |
22.22 |
0.2739973 |
502.4913763 |
| 0x239a9c2e1a96fb1b8a522bbd222426e7211f9bc2 |
21.9845 |
0.2760878 |
500.9588041 |
| 0xa8f0048a0d1a04663ca5010d0beac5bcaeea0eef |
21.7868 |
0.2945204 |
529.5987755 |
| 0xe0144fa05a0d32b5b1de10ccee7211616b3e3ef0 |
21.3095 |
0.2981679 |
524.4116119 |
| 0xceb1f665bee8283b36fbe282f36bff25124a206a |
20.9053 |
0.3007831 |
518.9768624 |
| 0xe0dd52618e72b11c371efe49a4516e18b29c92dd |
20.9051 |
0.2799171 |
482.9697227 |
| 0xfe6afe37c8563c653bacd30924d2251ea5bb9740 |
20.4778 |
0.2960998 |
500.4488277 |
| 0x6393c418a7cc325e48b109a7763fe0f318dcbc1a |
20.3509 |
0.2960998 |
497.3475694 |
| 0x512597eb36dcdf2e4fe85a69c9eec10a140013eb |
20.1 |
0.1991725 |
330.4178952 |
| 0x7adb8038758188dc51ae377a5f361bcd5c64e5c6 |
19.8063 |
0.3089107 |
504.9803744 |
| 0xe9be7b680a573fc03396f1227ea2695bc6dedfcb |
19.5297 |
0.2129502 |
343.2510945 |
| 0x79d3d692b3a08a5eb6144184cbc92a8dd97b71a7 |
19.416 |
0.2732351 |
437.8591622 |
| 0x04255bfb76851a262ad0af38eaabb828ca5c8123 |
19.3726 |
0.2984212 |
477.1510225 |
| 0x2eec756108603bfdf0b6c219d7e3ed10072e5927 |
19.321 |
0.2755477 |
439.4046714 |
| 0xb3ae363c083d2fdb4580733dc805b28f66f29d1f |
19.1497 |
0.2870054 |
453.6179109 |
| 0xa32aecda752cf4ef89956e83d60c04835d4fa867 |
19 |
0.2506274 |
393.025107 |
| 0x13bdf36d6982e6e9eb73b1aca0ff16f5bb1f17dc |
18.957 |
0.3083672 |
482.4763318 |
| 0x09129f15c61d63c80f3aabcacdea8be078cabe81 |
18.9208 |
0.2635847 |
411.6213064 |
| 0x6de73ed1941cbe37908817b582f0bd0c317e97e9 |
18.5997 |
0.1933713 |
296.8494288 |
| 0xe38ef24055bc6a7754c3f6811aaab97b1a9d01b8 |
18.3618 |
0.2990608 |
453.2241194 |
| 0x26aa7105b79d7ade6356e5fdd52fbdaf9f615c16 |
17.9188 |
0.1933713 |
285.9823301 |
| 0x0aecfbcd36b15dfb73d9ccaaeac1ebc3f8ace5a0 |
17.9187 |
0.2732276 |
404.0817296 |
| 0x693edbcf118ec982f5a8101498b6c789470b0b89 |
17.8067 |
0.2267277 |
333.2163047 |
| 0x0faeb89c3342dd5d248c1663b757f71a4d43c6a7 |
17.7524 |
0.275017 |
402.9533835 |
| 0xd0e6ffcd96033470482407d9e6bae762b71dbb3c |
17.6696 |
0.3081855 |
449.44566 |
| 0x34b09caadff3500de1aa060fc424286ab55d6640 |
17.3216 |
0.2728575 |
390.0875718 |
| 0x2aca2705f5718fe02c3740d3dfbc83025974e6e4 |
16.9836 |
0.2907683 |
407.5819632 |
| 0x58455cc7ad62e8416f3a822cee6d3a080f053e91 |
16.9537 |
0.2837105 |
396.9886503 |
| 0x0f2afb16f69f43c548bd049c46e3342fadc8a0d7 |
16.6819 |
0.2985431 |
411.0463221 |
| 0xec952ed8e7c2aa466cac36fd611d2e87df1243d7 |
16.3846 |
0.30824 |
416.8338781 |
| 0xf9bbd3597e5ab6ae14e5a11fef73d5d130bec230 |
16.2977 |
0.2663797 |
358.3155586 |
| 0x2a4677c01b9665b33e72227d15846eb6d38b2f24 |
16.0473 |
0.3037252 |
402.2731437 |
| 0xee62695710ff32dad6324146cd42b4802a717062 |
15.7785 |
0.3075891 |
400.5666756 |
| 0x23f80d3e457a73aab6088f613f6dbeed18731d2b |
15.7781 |
0.3064554 |
399.0802372 |
| 0x8e4c38089af04fd25eb64442024fa70ded9e5e66 |
15.735 |
0.3087867 |
401.0176483 |
| 0x51fb007343726cc4148a8adc9b755179f41d10ba |
15.58 |
0.298853 |
384.2937435 |
| 0x0527d7816ab05e35372c2432a72ccaacdb9fd6c5 |
15.496 |
0.3025223 |
386.9147205 |
| 0x4e4dee65c994905a087cd5a01d61446a2f01cadf |
15.3652 |
0.3044871 |
386.1404513 |
| 0xe920ed388234cf09d1826b7a12d2ac707b7f67fa |
15.3015 |
0.2906613 |
367.0788674 |
| 0x3663d35b69d1a290515e3471b03c4d68ff9584bb |
15.2309 |
0.30882 |
388.2122671 |
| 0xadcdd11d01338507dea594e194d1c316508a5fc8 |
15.039 |
0.302585 |
375.5818798 |
| 0xf145929a2f094840a797851cd306ae70c2b51986 |
15 |
0.2809882 |
347.8704908 |
| 0x5746396dfe7025190a7775df94b6e89310ddd238 |
14.9323 |
0.2930784 |
361.2008348 |
| 0x41477a57a8916237a8ff512ba3d9bf487d9cbb79 |
14.9323 |
0.2273019 |
280.1353458 |
| 0x48c73900c8941555717f19b16415c3eecbf4c00d |
14.8797 |
0.1991726 |
244.6030867 |
| 0x45a73cd17328c3e2849d3ad0f14fde749cbaef10 |
14.839 |
0.308246 |
377.5202613 |
| 0x9843800c65014c585105cf43936b9cc67ea9a004 |
14.8389 |
0.1991721 |
243.9318131 |
| 0x3d564563117e1cfd848dbc3c28beb19b50fd05f5 |
14.6335 |
0.2930739 |
353.9676338 |
| 0x36d36d3dcd05a28d3f018a96f61254b2e0eecd03 |
14.5865 |
0.3081894 |
371.0282383 |
| 0xa25aca28833b5d2e9ba5a649f3eb854b21727e07 |
14.5364 |
0.3081855 |
369.749285 |
| 0x28f1558d0cf03cd6fb852c0ca2bfcc43cda02464 |
14.4877 |
0.3084552 |
368.8330109 |
| 0xd66308eb23cc7e9d16f6d685de9a2c99de619051 |
14.199 |
0.2809523 |
329.2521614 |
| 0x0a7b367ee82e8a77fb2273f37848d4b8ad77bb57 |
13.985 |
0.3091128 |
356.794136 |
| 0xb237e39aac8b4b35924cf82f91c96e4ef9b493d8 |
13.9416 |
0.305528 |
351.5619273 |
| 0x46f8fffd5209e4226f712a7e7dc426a94f2df06c |
13.8951 |
0.2723415 |
312.3300506 |
| 0x710ae7a9fc19ac4ed64771d59ede7743a31c26bb |
13.8665 |
0.2503936 |
286.5684001 |
| 0x8cca36608c130f8fde914a392d3296271e365061 |
13.6437 |
0.2779239 |
312.9653346 |
| 0x61c2d89c9af7b775d041c5e00dd4b2698e1cb867 |
13.6176 |
0.2968982 |
333.6923887 |
| 0x21f72441b1ccdbdf40d2a834b56ccef55826d906 |
13.4662 |
0.3013481 |
334.9281768 |
| 0x57bd0b4bcab2748dd2a898de013f8b07fc9a7e3a |
13.374 |
0.3053947 |
337.1017913 |
| 0x5ed86506ff1244bb3ac0c309d5fc5ae6c0375464 |
13.285 |
0.3036365 |
332.9306767 |
| 0xb8070d71efd3f0dc24b7b0f51c69ccd167e703b7 |
13.2575 |
0.2767359 |
302.8066194 |
| 0x1f02c7c81c470ec06dd8822e64569b078f0ec079 |
13.2205 |
0.2930784 |
319.7937126 |
| 0xa25211b64d041f690c0c818183e32f28ba9647dd |
13.1849 |
0.2873713 |
312.721994 |
| 0x0cb0f554a2e8a5b7b5634f37840b037214925815 |
13.0277 |
0.3032305 |
326.0459986 |
| 0x3e37142870e7cf988e550db5711e82adf0a0d2c9 |
12.7717 |
0.3059364 |
322.4913417 |
| 0x38a7af58e2d293bb4e91f04945787aabd3c07e9c |
12.6232 |
0.2889486 |
301.0427915 |
| 0xdbaa3b4c5b1c5857857f27ac0bce9abf571aff35 |
12.6062 |
0.2794104 |
290.7133532 |
| 0x810eab519707de4ff325664d3d8acc8e736690c6 |
12.5231 |
0.3067813 |
317.0874108 |
| 0x7db223a235b08629b0ed0ead6bab25b12982c79b |
12.3548 |
0.3074755 |
313.5338775 |
| 0xafffd85357ee82009ab22b85381089c9ba984c17 |
12.2411 |
0.2901777 |
293.1721201 |
| 0x68f59a24be3b098ed549ff480df49538903cb49a |
12.2254 |
0.2713241 |
273.7724353 |
| 0xaeba2357a6f955728d3ca51598d372ba2ba08d77 |
12.165 |
0.2732278 |
274.3311947 |
| 0x255123a976393caf407b86971da20f09917befe8 |
12.1433 |
0.1933713 |
193.8059038 |
| 0x93e3d79dfa94b57526e050d10ae92b2bbea97c1b |
12.0898 |
0.1933713 |
192.9520489 |
| 0x89579b817f6bf1e05a8229b3aa1e7ab58dc8d05c |
11.9674 |
0.2721023 |
268.7634704 |
| 0xcb64ced0b772bd1a5737c4d3bfc87ceb55ccaf5c |
11.9667 |
0.2877795 |
284.2316627 |
| 0xdcb1ccf8db4305ddbf132ebb1103ed770d2fc359 |
11.9458 |
0.2749499 |
271.0859333 |
| 0x57cbc0f13eeed470813024735f92f8fa82bf25ec |
11.9458 |
0.2713241 |
267.5111446 |
| 0x05f761aacd63e4e96bf98f0fe5614de5ba90856c |
11.9164 |
0.2953279 |
290.4609282 |
| 0x7fdc01e1fcbf763495cb4f4514d9bf6bfddff740 |
11.9136 |
0.3027153 |
297.6566839 |
| 0xf4c6a5df9050b15a21aabccbc84ccb31fbdc0846 |
11.8838 |
0.281743 |
276.3419096 |
| 0x7b92ecc28fc91f1875263a8b1bfc707bbbb3bfd9 |
11.8712 |
0.2870054 |
281.2049307 |
| 0x3636c231168a725c53ee6ae3a669c1bcc946cbcb |
11.8659 |
0.1991725 |
195.0600331 |
| 0x6fb8346d9eedac5841332044e0942b60dcf74e52 |
11.6727 |
0.1933713 |
186.2951729 |
| 0xd0057c59a091eec3c825ff73f7065020baee3680 |
11.6035 |
0.2895198 |
277.2716985 |
| 0x3c0a5a0e4472798db80307888a092ec2dcb86644 |
11.5928 |
0.2451804 |
234.591509 |
| 0x660253b10fd7cea4be1133bddaa0d4be2a2790c5 |
11.5744 |
0.3083474 |
294.5621511 |
| 0x5009d2dcb5c808b5c636085b5ae90a1c9adc27af |
11.414 |
0.3069819 |
289.1937373 |
| 0xb7562f12e41c762cecda99d62bd6eac7b0c3b4c1 |
11.3612 |
0.3081792 |
288.9786648 |
| 0xa3072eb2348edb3324cb9c85aab1a47bb42a8486 |
11.3479 |
0.2828358 |
264.9037655 |
| 0x663c820ce0565075300ff0e86dd01577073f2ecd |
11.3033 |
0.2714858 |
253.2739877 |
| 0xbffb2fb17a30959dced1d0c1d7ba8af39afe9253 |
11.1531 |
0.3077762 |
283.314514 |
| 0xf9721228081edfcaeb68ca1f6c9e945f925e0c87 |
11.1454 |
0.3051571 |
280.7096949 |
| 0x016df31d2ba10863283dbcf1251cc52b333c7bd9 |
11.0658 |
0.3081557 |
281.4434706 |
| 0xe9dd7c08c47c5ba09da5daaaedcd5b181a8e7c27 |
10.9808 |
0.2555522 |
231.6071155 |
| 0x3333e73f33db57d3a5a2c5374f8402f2fcc15354 |
10.9794 |
0.3083445 |
279.417099 |
| 0xe588a2b38f24c72e30535885d645ceba44480d1b |
10.9356 |
0.3034155 |
273.853652 |
| 0x5a5d9ab7b1bd978f80909503ebb828879daca9c3 |
10.8638 |
0.2590913 |
232.3126645 |
| 0x0c8c74712fd60f82e08e3831ba6dbf5f1cbf021a |
10.8592 |
0.3074495 |
275.5559801 |
| 0xc1e224bc462cd451f7779ebaa034dd6ba066bec0 |
10.8458 |
0.2675643 |
239.5124039 |
| 0xad500eb3be8622b647b923c00dfc66577d7213b9 |
10.8103 |
0.30882 |
275.5379582 |
| 0x9eb4190a8a7cfcbd854ac86c0a7fe5c9351cfc20 |
10.793 |
0.2965347 |
264.153251 |
| 0x69b3381f8d6329fece58b547ec12e4c8ccb61163 |
10.7929 |
0.3084731 |
274.7854136 |
| 0xdd45b8f345768db3342d17d267fb18e76fae1e32 |
10.6092 |
0.3082458 |
269.9093692 |
| 0x6160e865f016a8ed6dcd5e75e15fe483ba53307e |
10.6076 |
0.2735703 |
239.5103227 |
| 0xbc4a9888cda0fab8f95f4b77f2d5b52c824bcb2b |
10.606 |
0.275017 |
240.7406079 |
| 0xf3f5e0ca82f167926af198af639629794865b532 |
10.5775 |
0.3084004 |
269.2378594 |
| 0xa30c3a65bae036024bca70d905951d00397d589b |
10.5565 |
0.3077716 |
268.1555194 |
| 0x0f92be065f77120d4fcff5efd0b64669aa779bbd |
10.5456 |
0.2991769 |
260.3979111 |
| 0xfd63b4eb4614b54d307f3e364a3630fe6b9f9094 |
10.4336 |
0.2732277 |
235.286566 |
| 0x544dfe1a52a7343d123dc5a0fb2f70cb425186b0 |
10.2876 |
0.2453399 |
208.3149313 |
| 0x220835ef29bd480f1ecabddf172ffb9a5d287896 |
10.2764 |
0.2731552 |
231.6800714 |
| 0xed17e4eb3b45fce0d5d4643eb704bafc29d440f9 |
10.2519 |
0.3053361 |
258.3572969 |
| 0x5299c7d2b73b6a96231081dabfd54dfcc84fedeb |
10.1892 |
0.2741621 |
230.5608927 |
| 0x46e0ac29855dc5d7209c6b51ab22089cbb113394 |
10.1763 |
0.3016735 |
253.3758884 |
| 0x0b4e8b7638f186f777d736204cd0834186e71d0b |
10.154 |
0.1991725 |
166.9185725 |
| 0xc8f663b727564ac460e438f306e74f8c9b36e3d9 |
10.154 |
0.1991725 |
166.9185725 |
| 0xbbd58b158dbde6fb1f32a32437e6a30abce72dc8 |
10.12 |
0.2400014 |
200.462234 |
| 0x7a8006d00668dc9445b5c06b48485cd51b65bb86 |
10.0484 |
0.3019192 |
250.3951497 |
| 0x5dca3693347f668488cd67f20922f7c650ed4deb |
10 |
0.2767358 |
228.4039595 |
| 0xe5a44cb50ea264362da8c254215f4bce15a3335d |
10 |
0.308817 |
254.8821682 |
| 0x5157d8ff3fcfacac630a1cb5bc9902dcc8433260 |
9.9395 |
0.2704952 |
221.9025521 |
| 0x5e499850ceae87aa52c5f454863c100787541557 |
9.9321 |
0.2969429 |
243.4177861 |
| 0x3c6eeab7aa300960f7d1bfdef472e22e14850903 |
9.8519 |
0.288013 |
234.1910686 |
| 0xa10d058252ddc859c67558a36932eace1e9d4cdd |
9.7937 |
0.2858572 |
231.0650182 |
| 0x4702f25d0870fb2b3efd50742d93243f57b7262b |
9.7937 |
0.2713241 |
219.3175775 |
| 0x6c926a8972ec6381d39b70eba165b0ababc07308 |
9.789 |
0.3077341 |
248.6292278 |
| 0x1ca98e3fdbfb777ececcd413e202b9cd2becfa11 |
9.75 |
0.2843705 |
228.8375965 |
| 0x03648bcb9a0f783c02ae27dbf6b5e4fdc4e1b203 |
9.7381 |
0.3048836 |
245.0453356 |
| 0x70796e8deea0cb8a962917a22c3883f0f595664b |
9.7121 |
0.3085588 |
247.3370885 |
| 0x3a57517491529b23c1ce90af715f9e8f8f0fb2a6 |
9.7091 |
0.3085177 |
247.2277631 |
| 0xf2393999f4d9cef25e3f474fa35e909355ad27bf |
9.7009 |
0.308688 |
247.155353 |
| 0xf99e247ee6a16297add60f7602c2d90436fde74c |
9.6158 |
0.3091225 |
245.3320361 |
| 0x1b858e7391c3feb82b3e28caf0b1c882a87f1ffa |
9.5608 |
0.241177 |
190.3129511 |
| 0xce0c16fb9df862074ba49ca2de11738b3ebeab60 |
9.4266 |
0.3092445 |
240.5998001 |
| 0x814abe8af088f7e6e6922439376d30dad8646471 |
9.2998 |
0.2589027 |
198.7231311 |
| 0xd1848b9fdbe2ef3eb48ecfabb49dfe6e3abc2997 |
9.2998 |
0.1933713 |
148.4239164 |
| 0xa6ecb5d7f7356ee2e64b15d36c1a25c6d3dc9932 |
9.2998 |
0.1933713 |
148.4239164 |
| 0x089315793c7f31083a00899d1503b38079dedad3 |
9.2879 |
0.2874652 |
220.3641897 |
| 0xc8d435b8fd811f0bffe62235383c69d529def5e7 |
9.2423 |
0.2937068 |
224.0434615 |
| 0x88c1d401bf50a7556ba0575ff62958161d231cf4 |
9.1809 |
0.3093941 |
234.4420541 |
| 0x9ef42f0f3b22df9aff84601a9def4f57b57bf83f |
9.1703 |
0.3059771 |
231.5851387 |
| 0xa7ad936f4613d0f04cbca84776c04d9f64e328bb |
9.1042 |
0.3048887 |
229.098043 |
| 0x839ae570815f727b00e4cb34ace93be11978b2a4 |
9.0303 |
0.2993789 |
223.1318382 |
| 0x334c6207252f6f9eff93a3de588195767628cd19 |
9 |
0.2363661 |
175.5762842 |
| 0x9b62a7ed23e6e2822ee8045694ef0db9eb099cc7 |
8.9984 |
0.2915746 |
216.547551 |
| 0x69ba4f7784574e42cfe0eb5e7babccd5c2d60d68 |
8.9972 |
0.3067317 |
227.7740381 |
| 0x961184f0b592e71690dba9447cfea60f0668cf5e |
8.9905 |
0.2831049 |
210.0726498 |
| 0x74b35a2fd229534d71c67c13aa1c075b96a1e7dc |
8.9284 |
0.3020819 |
222.6058413 |
| 0x63f20d7d378fe34fdd03ca2c09040ca96e36e10b |
8.9034 |
0.2894931 |
212.7317199 |
| 0x3f3b90597cb7adc5fe7ccbe4eb22a0f7a34388c6 |
8.9034 |
0.3083735 |
226.6058944 |
| 0x03e054022d3756429bbfc17e788a44781b221649 |
8.8714 |
0.2871728 |
210.2682321 |
| 0x4ba277699f2ec1a0dfcb65f01abe65803ab3d4d0 |
8.8714 |
0.2927649 |
214.3627487 |
| 0x281756ff1ad5bb1109ea472e5eb282395677fffd |
8.834 |
0.30882 |
225.1651045 |
| 0x8c1906750e4f0c7b81172dced02f33d013695a80 |
8.8222 |
0.3002862 |
218.6504791 |
| 0xc2b8d0e853a2b0b8401f93fce9f80c67c089907c |
8.804 |
0.304137 |
220.9976032 |
| 0x3e584b87ccb4a59e5c676a150c0407164315c076 |
8.7966 |
0.3086673 |
224.1009268 |
| 0x037f29ce01d56a51829b78acb0702763d542bbec |
8.75 |
0.2529174 |
182.6522354 |
| 0x7bc1d6e8150d4c96917901c26c922dd64654b3c3 |
8.7153 |
0.2981679 |
214.4773472 |
| 0xb93299607be4b4d26d533f2cb6419db7da570920 |
8.6132 |
0.2957824 |
210.2688833 |
| 0xcb1be9266a727a0cf7b95f0d0efbe73c2717a5a4 |
8.6024 |
0.2936827 |
208.5144716 |
| 0x6a28d159d8fd5f164da44082851abc23ba8a922f |
8.5861 |
0.2860321 |
202.6977473 |
| 0x01c5063f21def1ea78728303fb07c31b0375a2b1 |
8.4921 |
0.30824 |
216.0440288 |
| 0xad63a9ef527376d84a50f2eae49ef020cb5b46a7 |
8.4582 |
0.2960998 |
206.7065943 |
| 0x74253dd4697b80067b920c94a151f12f148792aa |
8.4345 |
0.275017 |
191.4507518 |
| 0xa4510dad288fc2da301cdefd44a289e2469d2788 |
8.4088 |
0.2719168 |
188.7158084 |
| 0x95e3469e6adb95798f294f45896cbcb8c17486df |
8.4003 |
0.2261547 |
156.797312 |
| 0x0dc6f4eab35d7d896ef869d4381c766b4929290a |
8.324 |
0.2714993 |
186.525835 |
| 0x270735e7afdc9ef0ee9f3186990fd118e253dcc1 |
8.266 |
0.3082098 |
210.271306 |
| 0x46e1a9103d9fb3cf6b9ce4702d960b63a1bf02e4 |
8.2533 |
0.3086915 |
210.2764163 |
| 0x7dadf796a1496e02c170f977fe18cbb6d6ec2f25 |
8.2232 |
0.3081919 |
209.1704173 |
| 0x7bd83885010522a96c32fd1db6eaf8c69b05074b |
8.1197 |
0.3092415 |
207.2411362 |
| 0x4be828f2e43a3bd9348e0c44416e4a3ed756842c |
8.0547 |
0.30882 |
205.301944 |
| 0x690a8f4592a2cd0715865e8600c1f48bc4eb1d4b |
8 |
0.3093941 |
204.2867728 |
| 0x272c5f981e19820348e4290bb80a0c791e877080 |
7.9455 |
0.3081972 |
202.1101771 |
| 0x67eef0911861ebc1df7ed07860aee4b618918461 |
7.944 |
0.3054135 |
200.2468423 |
| 0xf3c6ccf02ffecda1557540fe1b9482e25f3b83c4 |
7.9373 |
0.3045345 |
199.5021436 |
| 0xcbf27d934ce7ae298baee41acf9a8a33dbc77dfd |
7.9272 |
0.30824 |
201.6726459 |
| 0x3d35b9c05b3a85e6901c7eb5ed4688cd8f9fe1a4 |
7.9109 |
0.2927561 |
191.148152 |
| 0xdde3a0db070c7252e1785d804176f3461657e693 |
7.8045 |
0.3086519 |
198.816404 |
| 0xe7e3884efd3955789c4baec29c081bb61ded8015 |
7.785 |
0.3093941 |
198.7965658 |
| 0xe44d51836e6eda3034a4ff13ee5b47c8125ee278 |
7.7732 |
0.2706749 |
173.6545139 |
| 0x9ad3bed8365d6a8ffb6529428901cbc74bc57d9b |
7.7689 |
0.3005584 |
192.719893 |
| 0x89d0cade40d40981f0c08b2c9eec5d68eb4d5e15 |
7.7525 |
0.308246 |
197.2320068 |
| 0xd5e95da7b70b1b1c4e243276ead095edc0a10b49 |
7.7508 |
0.3087256 |
197.4955719 |
| 0x56be1daf69e487f2fe10fcc3575b2096a2a1b5bd |
7.7344 |
0.2437126 |
155.576057 |
| 0x07d65bfefc28f145f5fe0b6391f1fc76d7fdc498 |
7.6957 |
0.3087898 |
196.132395 |
| 0x87f1c862c166b0ceb79da7ad8d0864d53468d076 |
7.6948 |
0.2735444 |
173.7254014 |
| 0x1720297747aaf387a0a6d760174880df2771f83b |
7.6742 |
0.274049 |
173.5799364 |
| 0x84e4a60ce6def11eb259f20cd775e27383e51811 |
7.6507 |
0.3085445 |
194.8305999 |
| 0xea4c9a4a66f4150e6bcf53040326ba578e948692 |
7.6231 |
0.2713241 |
170.7097232 |
| 0x67c015912d26b1d389c351f03fd8a83106d6b788 |
7.6059 |
0.3087793 |
193.8371501 |
| 0x41b4b4be53f064dd5eaeb4c885cfc3b149b02935 |
7.5494 |
0.3080905 |
191.968041 |
| 0x59eb4a252024cdb00310da56fae5bf0ad2827013 |
7.4793 |
0.2734794 |
168.8199397 |
| 0x95ef39e2703bd0b55db933e65fbdea4a7ebcb793 |
7.4792 |
0.3090845 |
190.7965873 |
| 0x38f80f8f76b1c44b2beefb63bb561f570fb6ddb6 |
7.4532 |
0.3037845 |
186.873014 |
| 0x517f8726bab42a606497ca37b4bc18bc1585ff1f |
7.42 |
0.2735668 |
167.53496 |
| 0xc091b305b1857d2482aff07f7628596405923e45 |
7.4031 |
0.3080937 |
188.2498717 |
| 0xbda960d127b16e0bc41af677415bed516715f09c |
7.3805 |
0.3048015 |
185.6697426 |
| 0x3f1f6c7b1f39c662525b3138822763417c7b11c5 |
7.3642 |
0.3075313 |
186.91887 |
| 0x1916db2419f06a5e351df2e7eb376caa9c424c7f |
7.3494 |
0.3093941 |
187.673151 |
| 0x4d4025858175850aa10fc228d06c4c3ac765d25f |
7.3494 |
0.3093941 |
187.673151 |
| 0xb02daa162019ad753718359c3aacf8120a8ef4a1 |
7.2981 |
0.2735249 |
164.7573685 |
| 0xd3d2f7704fe3836c7ce3b91e45e727368361d911 |
7.2759 |
0.3081557 |
185.0525571 |
| 0x6884fa21b4c3715613ff1f27c684faf0fa0c7501 |
7.2706 |
0.3085401 |
185.1484506 |
| 0x8a4a50b13fd2cb36feb96c408cb98b4c9f2b8f25 |
7.2623 |
0.3089548 |
185.1856563 |
| 0x8ce01cf638681e12affd10e2feb1e7e3c50b7509 |
7.1955 |
0.30882 |
183.4022552 |
| 0xb06206d76e1fdd39ed540678f40170f6d97c1272 |
7.1944 |
0.3085235 |
183.1981248 |
| 0x3609ca4b9583fa16fa125993d484d6700b358e2f |
7.1668 |
0.3051179 |
180.4808745 |
| 0x20e77575e23c750596fc66bd69e7674b2d29ccc9 |
7.1579 |
0.308246 |
182.1047405 |
| 0x4a627a6f1fa80cf6c9891040456f4b4438f25471 |
7.1461 |
0.258515 |
152.4730526 |
| 0x39d384866d92a40a347c61a2c5f9946aa3feb0b3 |
7.0991 |
0.3081318 |
180.5419084 |
| 0xbd63144c19379a62699f9544836cfdf05a3c31ed |
7.0925 |
0.3089107 |
180.8300038 |
| 0xc749dc90d596e5febc3f5c191009779ee44e77d7 |
7.0917 |
0.2960998 |
173.3112419 |
| 0xc44c689fd7796e3ca636f05ae477f1a46f30ceaa |
7.0757 |
0.3093941 |
180.6839898 |
| 0x588ffac7afb5d4524efb7eac1d7dfd609ce5dea0 |
7.0461 |
0.2735576 |
159.0874274 |
| 0xac77727bcaf7fd536279021126ed43995752d325 |
7.0214 |
0.3084969 |
178.7774197 |
| 0x3f7a9ec39d25c310faa8ef4bfbecf1c61ec13865 |
7.0159 |
0.3078581 |
178.2675263 |
| 0x6ed274ff7c1c0c3adedb7436b868552023f65a78 |
6.9719 |
0.3084625 |
177.4972821 |
| 0x61c0e8c8d3133ff09a03b2118812d4e82a52be98 |
6.9454 |
0.3025004 |
173.4049457 |
| 0x374b66f535d46441ddf81e553fa19ab148a23dd2 |
6.9446 |
0.2732275 |
156.6065082 |
| 0xeb9a747ce5dfe42b834085af5186232bdb4bd535 |
6.9342 |
0.2935926 |
168.0272624 |
| 0x5869699c85d5d7be8f0261c0ab6e703120a4af95 |
6.9084 |
0.3070375 |
175.0681273 |
| 0xffb3a07089f7689e1fb57f121cc6a3fe6d8f2598 |
6.9038 |
0.3082754 |
175.6569424 |
| 0x83b01c3a08efd868f67b5ab2c6a62fc998b8a9b8 |
6.8996 |
0.308857 |
175.8812429 |
| 0x05195b4d785faba6ddf83e907666ee8e180291d3 |
6.8698 |
0.298482 |
169.2390213 |
| 0xcf5d6cee3ba0591da6c28479cbc54e100d121756 |
6.8619 |
0.3075241 |
174.1653266 |
| 0x7261c1168b8ffec771de760bf55dafa68c8ed56d |
6.8568 |
0.308246 |
174.4444238 |
| 0x7b06ae8099bf09c530ca28bc8431727fb845defd |
6.8116 |
0.2758186 |
155.0639579 |
| 0xa7c89995b915d7416ae3adfbc60f5aa9fd995e87 |
6.7938 |
0.3072066 |
172.2588203 |
| 0x0055e76d319eebe5f3afe7e7a8c62767d4cfff01 |
6.7656 |
0.3082576 |
172.1307101 |
| 0xfe878e49a8b2b4c2c9bd5943f3d0126f4c23fa8c |
6.7583 |
0.3048015 |
170.0171879 |
| 0x8c7d025fdbd4e5cd671dc3c19c9060f9436a7627 |
6.7439 |
0.3046112 |
169.5489658 |
| 0xd19839edae87b617cfc24c059b4eee264e2d1cdf |
6.7228 |
0.3082703 |
171.0488329 |
| 0x6f834a4b9f42aac14aecd50e145a30f9779aeab4 |
6.6911 |
0.3076595 |
169.9049706 |
| 0xf4468d8f535bd91440f7f6fa91d0f97dbd044472 |
6.6817 |
0.3060371 |
168.7715653 |
| 0x6057cc69ebd4746120c47489d322f26028508fe6 |
6.6629 |
0.3082941 |
169.5378609 |
| 0xcfc786cd276f57e1462c27ecb09735b86caf53dd |
6.6627 |
0.2758183 |
151.6741732 |
| 0x972d8bab2826fd9bd453cdc4058a4b5be7ae43ce |
6.6523 |
0.30882 |
169.5569202 |
| 0x765b164b32c295af2eec1d94a84871668a4ffe9f |
6.6474 |
0.2906301 |
159.4522325 |
| 0x1cfaeac9abfbbda55fc63e7b11f51110e635563d |
6.6438 |
0.2755712 |
151.1083787 |
| 0xfa3adf7bce27b5f4c5b9322098f7b5059fe545df |
6.641 |
0.2841118 |
155.7259428 |
| 0x4638aedf9c02eef5b8288dcfb6b5f2834fa78718 |
6.6406 |
0.2814683 |
154.2676928 |
| 0x762a60c99107e42be148aad20dbc6e0ec16ccf38 |
6.603 |
0.3088789 |
168.3324413 |
| 0x98c700427f538e3791747ff481226b2543443440 |
6.5251 |
0.2790311 |
150.2719839 |
| 0x836eb99ad1bc73bc61d405a0df81bbe168055c27 |
6.5172 |
0.3083231 |
165.8461468 |
| 0x1fd2a56907b1db9b29c2d8f0037b6d4e104f5711 |
6.5099 |
0.2967099 |
159.4206479 |
| 0xac4bd00ccb3e001a4603f5f85bfbc31018af914f |
6.5099 |
0.1933713 |
103.8973799 |
| 0x73c18ddde43b36469095affcc1596fc861a6ea1e |
6.4617 |
0.3025742 |
161.3677849 |
| 0x2905023c933944c027acceaf0f92c8a58fd1815f |
6.43 |
0.3052934 |
162.0192682 |
| 0xcb5722a78d17a4b241fdd717fd1864d24043f8a7 |
6.4261 |
0.2794992 |
148.2402881 |
| 0x3eb0a1cd9e30adc88bee5c1bff74d19191496fd1 |
6.4215 |
0.3012049 |
159.638143 |
| 0x93df5c93f0d5599664b16d4c6bf248da7df1e343 |
6.4192 |
0.2735895 |
144.9501284 |
| 0x92b8417cea2b996b62e5d01ad16e9816a3f6f010 |
6.4192 |
0.2735895 |
144.9501284 |
| 0xd7542dc0f58095064bfef6117fac82e4c5504d28 |
6.4013 |
0.3087423 |
163.1182448 |
| 0xe2fa3b1deb049aefbdde15c350d2f177d38b2252 |
6.3999 |
0.3050433 |
161.1286832 |
| 0x4fb20bc374658feb1fddec6c6de78c6dae8e042c |
6.371 |
0.2729734 |
143.5377407 |
| 0x42924575e2d84fe4107f0452777cf61bb68645bc |
6.3636 |
0.2738188 |
143.8150664 |
| 0x21e6acf76878f2d691f13ff291d9218b3f30cab1 |
6.3598 |
0.3087581 |
162.0690535 |
| 0xff3718c8a8c1ae1f7614a0f8c0cef59cfaaf573c |
6.3467 |
0.3082681 |
161.478537 |
| 0xa551066e1a04975117958f9ee8657ca33dcc072e |
6.3372 |
0.2715508 |
142.0321791 |
| 0x0f18f33bb00127e1803cf0e14e5f863450428d16 |
6.332 |
0.2732276 |
142.7919535 |
| 0xcf9b5f837a4700cc169dc4d63c8b353ef950668a |
6.3223 |
0.3087462 |
161.1071724 |
| 0x7e946e8060434f1987547a7a8ff1d8963bdda2b0 |
6.3087 |
0.2704473 |
140.8188306 |
| 0xb9dc5f5b15500bb0dff235911a3a7435c8240b6d |
6.27 |
0.3088054 |
159.8051188 |
| 0xaf6595ea2460ed81ca81a424240a18c3168d1766 |
6.2469 |
0.3079684 |
158.7847925 |
| 0x64aad320909c5dc89cdeab958824284eeeb63a0d |
6.2459 |
0.305739 |
157.610134 |
| 0xc80c03284882defc74686c89a21e3ddc327b7c86 |
6.2434 |
0.3087423 |
159.0946317 |
| 0x6c7d0ee04194e8c0be559fc0d9ee4240cf66b0c6 |
6.2425 |
0.2780834 |
143.2754492 |
| 0xe5c7c579587b3227d4532da07336a17d36bd0cb6 |
6.239 |
0.3020339 |
155.5281326 |
| 0xcae4ccfe670f8c2a4999f9dfaf44625110fce9e5 |
6.228 |
0.2961905 |
152.250214 |
| 0x79f80858bd5dd39fcb5e5cb3ff7ec40a818cafc6 |
6.2069 |
0.3088595 |
158.2245935 |
| 0x6e78b133945b3c1862e7c61a7c984e2c06350388 |
6.2011 |
0.1951319 |
99.8700577 |
| 0x29771302b9201f8540e39109b36ba44d2ddfdf05 |
6.1918 |
0.3026689 |
154.6759886 |
| 0x3d32961f12b010c1270981aea4491f4034052ba6 |
6.1886 |
0.3081456 |
157.3934081 |
| 0x1e92ea4e63182c06aa0049502de0cf80e3c3a773 |
6.1776 |
0.308882 |
157.489142 |
| 0x2eeaa7534aa31545e98319ed72827da53264775f |
6.1774 |
0.30882 |
157.4524501 |
| 0x9c16abde3c6faa11567cd082dcb7ba51d84c67da |
6.1774 |
0.30882 |
157.4524501 |
| 0x2273d11720c89598e4e4d1f85825538c9b9151ed |
6.1774 |
0.3007831 |
153.3547926 |
| 0xa5374feecd275c374a26fbc1f5f1ed89c7c40308 |
6.1772 |
0.2835606 |
144.5692197 |
| 0x1a5a3b33c050d86929a197ce117fbb6af0f15bcf |
6.1725 |
0.308246 |
157.0350923 |
| 0xe7d23ef72efa2342c7835ded9e252c155e06fe13 |
6.1679 |
0.2732277 |
139.0913784 |
| 0xaa717eefa70c7526306a485284b94b54a6aae9e8 |
6.1553 |
0.2736156 |
139.0043044 |
| 0xe37a845fb8ad56ff347c848af9f4557bf402940d |
6.1553 |
0.2736156 |
139.0043044 |
| 0x186c5d3d9137d98501db8410dad139c7875fe4fe |
6.1512 |
0.3093941 |
157.0760996 |
| 0xb7412e73dc7a0824f97d784be3177fdf25673a48 |
6.1419 |
0.3087898 |
156.5322914 |
| 0x35be0cc858adc4393fb95edb7b9e14ebdc2cfc0f |
6.1403 |
0.3069163 |
155.5420305 |
| 0x2524869f385b9d01b1e5a12d5e6e0fbcaa4d577f |
6.1337 |
0.22518 |
113.996271 |
| 0xfea8a0c6daeeb1f150c0694aa214224e47a9b8d7 |
6.1206 |
0.3065237 |
154.8446944 |
| 0x495e4f8c59f9b2df760f77c42f27ea514697bf73 |
6.1206 |
0.2713241 |
137.0631268 |
| 0x325fc6333ccb80bbeca15a5665c33868ec40e335 |
6.1203 |
0.30882 |
155.9970537 |
| 0xb29da577ee292c7d821927b6b95090e1d90fe169 |
6.1052 |
0.2893817 |
145.8173321 |
| 0xf6b1d07055f2caaf862b78cbcb9c5b1325acb22e |
6.0993 |
0.2732272 |
137.5441711 |
| 0xc19b96baf4e13110e7fdd927ff24b40751c3b3ca |
6.0969 |
0.2714097 |
136.5754432 |
| 0x85da67cbeb68bf3ce7ea3682b69a860aa8a7eec8 |
6.0879 |
0.2732277 |
137.2873092 |
| 0x9f99f220094a89f1d4a5ca8d09df26783be48115 |
6.0843 |
0.3087424 |
155.0404617 |
| 0x5ddd9a22670a98e8f137099b53c0c5c370be45a3 |
6.0674 |
0.2730496 |
136.7358626 |
| 0xf37d53203e5e0ba9e72df40490bf86ac2742f885 |
6.0609 |
0.2732273 |
136.6782792 |
| 0x4bd1b7ae8e4ff6802dc17865fc92d8760100d35c |
6.0593 |
0.2972168 |
148.6394294 |
| 0xe2598cb22ee63975ee448f33d45cde8dcdcd3f76 |
6.0531 |
0.3052798 |
152.5155379 |
| 0x35edeee56ee03e1363f1cc8acd5186c5b9ced325 |
6.0414 |
0.30882 |
153.9860164 |
| 0x593621ddfbe1811f3cdd811e9b5b86ff6778ee25 |
6.0371 |
0.3076629 |
153.2998459 |
| 0xf7e8610fef40286a898c627c65e5164a3eb3a232 |
6.028 |
0.3088793 |
153.6739811 |
| 0x724ec44d80a68f08b1ef58fc1c5e2347bcc1c2a0 |
6.0255 |
0.308817 |
153.5792527 |
| 0x848dd32098489e02b836ba40d1441f3a8a9ae65f |
6.0254 |
0.2954228 |
146.9156576 |
| 0x7c1f76c4c99220da4183b9e896533a38eb7ab247 |
6.0196 |
0.308659 |
153.3503653 |
| 0x4e7b0567785f25cb27c2ea71f543d4a14d6b9580 |
6.0026 |
0.2760653 |
136.7695539 |
| 0xd6b4c44d0690c6dbc1f4c4bddaead52486a30aba |
6.0021 |
0.3087981 |
152.9734626 |
| 0xd1ffda9c225ddee34f0837bf4d4a441bdd54c473 |
6 |
0.2619107 |
129.700823 |
| 0x0228d60c470c015cd3531cac465b53457bc4c08e |
5.9979 |
0.2938942 |
145.4884304 |
| 0x179419df1d8ad5134806a5af394b108138ad885f |
5.9979 |
0.3082869 |
152.6133306 |
| 0x5adb2e64653041f6c027124fa46aeae039b7647a |
5.9863 |
0.271763 |
134.2724705 |
| 0xa9ce363e7efa49c12038ca361616139ff477857c |
5.9834 |
0.2696335 |
133.1557975 |
| 0x8afc051de5f3941a68d3dbb9c7c96ec773ef494b |
5.9796 |
0.2972755 |
146.7133147 |
| 0x9d5aa3c262fdb773423fcff4335e559543764f86 |
5.9729 |
0.3081601 |
151.9147432 |
| 0x3613da05428b2523b78ba608ee01692a0526ab86 |
5.9729 |
0.2732273 |
134.6938056 |
| 0xe8995aee06f518de9865917ead8aa489d1034649 |
5.9729 |
0.2915978 |
143.749934 |
| 0x953d9a5a14fcd2c9856f9bf9f0afca955c68041f |
5.9729 |
0.2870052 |
141.4859003 |
| 0x4a0a41f0278c732562e2a09008dfb0e4b9189eb3 |
5.9729 |
0.2930784 |
144.4798506 |
| 0x0865c5de7fe349aa5b7f6ef721f8c2b9cfe5e40d |
5.9729 |
0.2732273 |
134.6938056 |
| 0x157009ad5f3d68f35159bb5716f887728fabaad8 |
5.9729 |
0.2967644 |
146.2969687 |
| 0x1f6ab63df84ccaac1cfbd00508003f8f0b1f41d6 |
5.9729 |
0.2732273 |
134.6938056 |
| 0x7dc0c8a59912dad647d1a45e961817641c9c30b6 |
5.9659 |
0.2818925 |
138.8026446 |
| 0x883fa0e8adb811adbf7364a3ae8270115aff5f32 |
5.9506 |
0.3089107 |
151.7161797 |
| 0x96dab34cd9cd05ab159c281e85fbca5c6045eec8 |
5.9449 |
0.3087587 |
151.4962905 |
| 0xcbc09041414cb8e431a1df78baeb09fee4b7a572 |
5.9404 |
0.2718503 |
133.2857718 |
| 0xd35a3a363342b1ab717a4cf0f2ffea70b43c9df0 |
5.9356 |
0.3080646 |
150.9192602 |
| 0x801ca888631c27be9bf1d488b85a1bfb372e596c |
5.9356 |
0.2732278 |
133.8528623 |
| 0xbcdb165940a6d706e0d3da8c04db51cba1cfbcd0 |
5.9356 |
0.308246 |
151.0081058 |
| 0x20ef214ea30d5aad1877e07cfdb6d9784b377dcd |
5.9356 |
0.3066748 |
150.2384075 |
| 0x6d4273f5335299599d8fefc850ef3483a7ad7b59 |
5.9229 |
0.2800753 |
136.9138729 |
| 0xd8c66503d2e42acce57783a9cf2c5cdb76edc721 |
5.9226 |
0.3084653 |
150.7845777 |
| 0x45ba8ab4d29d654366ec958c5ee99a708ed63e0b |
5.9224 |
0.2716214 |
132.769986 |
| 0x540ef425920b64cafa189ddc9cf3abe49a318fe8 |
5.9224 |
0.3093941 |
151.2334979 |
| 0xd82df8edb6625ed6223e0f52c040d5443a5fbee0 |
5.8882 |
0.3087358 |
150.0402302 |
| 0x4f8d9db539d1fbcb43aad915f10fafd46c7a9591 |
5.8852 |
0.2785112 |
135.2826335 |
| 0x9b37bc27b829861eb16b9537f162be3f20510923 |
5.8823 |
0.2231363 |
108.3317307 |
| 0x38a49bb53bc5346121fd4ec1ce943ad4d5f1e98e |
5.8795 |
0.3076629 |
149.2979127 |
| 0xd3d1d6e23ea9ae3103de17578ed32ab54a26bdc8 |
5.8572 |
0.3087657 |
149.2647703 |
| 0xf4e0a10d5659d212d0bd3aeefb43ad19b5471b5c |
5.8464 |
0.3041473 |
146.761038 |
| 0x24424d7a3667fc684849ffe146d3336eb0103303 |
5.8428 |
0.3085842 |
148.8102674 |
| 0x8c82e506f39aeee8f8852b4f1a9f2410f72185e9 |
5.8393 |
0.303572 |
146.3055328 |
| 0x6de554b5f8c5020f458969bc73ba2383c3894654 |
5.8165 |
0.2767712 |
132.8681139 |
| 0x85c0c67690a91419057d831c2b773f2e5e6a6386 |
5.8146 |
0.3087898 |
148.1907326 |
| 0xe43bd4b74614391c28c21dfb3ac1e91bb03e5047 |
5.8102 |
0.3088838 |
148.1236691 |
| 0x8b83b7028b4d79f18aea106b2f8a0dc7c35ca122 |
5.8102 |
0.2767358 |
132.707238 |
| 0xb3a84330b0c3cd838d9ed9edc59574207d6825d4 |
5.7938 |
0.1933713 |
92.4684925 |
| 0x0dad260305b3e6ed940240caeb5169aaed6727eb |
5.7588 |
0.3088181 |
146.7820381 |
| 0x05e14e44e3b296f12b21790cde834bce5be5b8e0 |
5.7564 |
0.3093941 |
146.9945474 |
| 0x1fcb78eeac267eff8dec5f9ddfd881e710d1821b |
5.7227 |
0.2715523 |
128.2604353 |
| 0x595c41c83c249310146ad7556cfdc6a6cbeb753a |
5.7182 |
0.2809702 |
132.6043541 |
| 0x13ded954f8d75be0ce84807e0d3b94e4b9bccbf0 |
5.7156 |
0.2719183 |
128.2739342 |
| 0x2eed6d9f252f2ca92e27007142786149fc7827aa |
5.7 |
0.3087927 |
145.2714044 |
| 0xdc2fce5a7c3978080992529a2afa741e2a13009e |
5.7 |
0.3087866 |
145.2685476 |
| 0x79040bff41ee0c863bb1f0569320d3b5f6dfbd56 |
5.7 |
0.3087866 |
145.2685476 |
| 0x8b67305dcd897d380498bf38c9a1992bfafab763 |
5.7 |
0.3087866 |
145.2685476 |
| 0x17d6358b32b71da266e050e6cb1de0316ec0357d |
5.6876 |
0.3045345 |
142.9564682 |
| 0xa2fb6967a323cef8b481e88b39539fbc22d61e09 |
5.6762 |
0.3080905 |
144.3358412 |
| 0xe2695c1d17ea9703669cc0d57a40441cb1504071 |
5.6762 |
0.285277 |
133.648068 |
| 0x9e716dcba3165044d1717c8ca26ebee94e8fbfc0 |
5.6743 |
0.2732275 |
127.9602167 |
| 0x32a38f97c8c65fea977eb3ac4cd3effcdcfa9bcc |
5.674 |
0.3084612 |
144.4535264 |
| 0xfbe46f0eb44c9e8da8fabfbe41450ae78a64251f |
5.6622 |
0.2717412 |
126.9927241 |
| 0x06716380eb219d26adc66aabc7226ffa4a6f7ae1 |
5.653 |
0.3029538 |
141.3492612 |
| 0xfdf007d8261e5e7e86751a22b1fe1c4a3b7b2b93 |
5.6524 |
0.3081873 |
143.7758242 |
| 0xe2d32ca944a15df956adc05ee5f30cd746d12aeb |
5.6494 |
0.3067972 |
143.0513562 |
| 0x32cbe183b33302b88045ab40042cfa7e9f24a9c9 |
5.6488 |
0.3075718 |
143.3972712 |
| 0x70e9e9c0c221ae0dd3c66787cef1bae044ee541c |
5.6488 |
0.2717323 |
126.68804 |
| 0x469f7fab9343857e0ace8be9a5169ac24b24e396 |
5.6463 |
0.3063946 |
142.7852472 |
| 0xed00498c24e52645cf4567af1531b1e653ef1fb9 |
5.6264 |
0.2673629 |
124.1566332 |
| 0xf527e46892336f2a3c732b999b18f619d7b5e6bf |
5.6204 |
0.3087898 |
143.2413557 |
| 0x11849573966d4a16c2196d32e79164087b23e202 |
5.6112 |
0.2717323 |
125.8447697 |
| 0x0be7edb81f3f05ccb90a32e74575488756c31968 |
5.6024 |
0.308817 |
142.7951838 |
| 0x56f6a22b5283570bbdce089a482912789a3c4bca |
5.5925 |
0.2789343 |
128.7496893 |
| 0x6b12f9db268ee3dd251a6daa7f03f114c628a71c |
5.5848 |
0.3093941 |
142.6125961 |
| 0x35c1ad326b37ba4451a2a669a5fc03a1c339dd81 |
5.5799 |
0.2734361 |
125.927458 |
| 0x5e18e1fe3e046670c59012769ea386be649001fb |
5.5799 |
0.1945316 |
89.5890066 |
| 0x76ca1f2bc011846f6c6f6fe2d8f77603ca76b7a7 |
5.5782 |
0.2718143 |
125.1424318 |
| 0x235c58a9ff01c10c9e2fb10361e592f84912ee1b |
5.5596 |
0.266913 |
122.4761447 |
| 0x71559b4f4c96184d1f9699222f7df16a4cd3323b |
5.5596 |
0.3007831 |
138.0178195 |
| 0x38aa050840987daab8bd03e77bd71f8bbceab748 |
5.5596 |
0.283561 |
130.115273 |
| 0xad14b66ea4a2eba91947316d0e05f604b5cd2457 |
5.5596 |
0.3092347 |
141.895923 |
| 0x31411a6a4160ed5b9ac62910bb86c90b0450bae1 |
5.5592 |
0.2736455 |
125.5563998 |
| 0x28f068a5eea3af03285480b378c68511375be0b4 |
5.5524 |
0.3078471 |
141.0763117 |
| 0x88c0c80eb5436a6fb83cb7b181ea713e1c9bb37a |
5.5523 |
0.2716214 |
124.4729968 |
| 0x0e28a9b248e85bda922d9ef0a4fa9d8a786aa699 |
5.5523 |
0.3075364 |
140.931383 |
| 0xb4f3f016db62d15390a06510fc014c0d299fd36a |
5.5523 |
0.3090465 |
141.6233789 |
| 0x62382761357bcf73d17f3b124799e59476a0bddf |
5.5505 |
0.2736152 |
125.3460131 |
| 0x9390163de4f8d74208bb2a527c088b189af803af |
5.5485 |
0.2709915 |
124.099318 |
| 0x8127cb8091a5d9398b33245c4633c11eafaf3d4e |
5.5414 |
0.2550084 |
116.6305297 |
| 0x589cc1a3bd0d4107803198f5e81ba60aea43d8da |
5.5354 |
0.2732278 |
124.8280472 |
| 0xdcf98b00ad5c61739f5762f6241a872ac1e0217e |
5.5335 |
0.3093941 |
141.3026072 |
| 0x3df9aa7083ffa957b6b83c8514a792ce38c57e22 |
5.5328 |
0.2765077 |
126.2671486 |
| 0xf9bae0bdcb7c0af0409b4fd31ad880398f988709 |
5.5321 |
0.2732276 |
124.7535177 |
| 0x6e0a064722656d7921295bcfa3bd76225dafc9b7 |
5.5085 |
0.2818386 |
128.1362449 |
| 0x79600a3805deb56c46a000678c3883abbe69e436 |
5.5085 |
0.30882 |
140.4032123 |
| 0xe622ae34c62856a3bea964b1b0023a7bf787214c |
5.5063 |
0.3072328 |
139.6257735 |
| 0xb87dc8638aef77b69fc2d2cbbb38e4486df5eaba |
5.496 |
0.3088123 |
140.0810936 |
| 0x04a20d242167c24cc162f76afe2daecf09f44f5d |
5.4924 |
0.2822714 |
127.957944 |
| 0x6588a19e688d1359db1af5837c1ffab1611e110c |
5.4867 |
0.2894527 |
131.0771605 |
| 0xf2509a79f13e6d6904827363fca7898b63e8f7a6 |
5.482 |
0.308817 |
139.7264071 |
| 0xf98162fd059525872a3d28a6f3ca296689f5dcdc |
5.482 |
0.2822715 |
127.7156982 |
| 0xc9dee42e833664df938d6ef1b85af30e5dfc62f5 |
5.4553 |
0.2901115 |
130.6236502 |
| 0xe193440c415fd35ede763dc2c0a4c1a53b526109 |
5.4377 |
0.3065087 |
137.5613152 |
| 0x6058deefb60b2f5d25f949eaff69abbc1f97f3da |
5.4281 |
0.301337 |
135.0014583 |
| 0xf7d62bcd4e75d8f3981b49bed5c926f17e877597 |
5.421 |
0.308367 |
137.970275 |
| 0x44a16066b07d1ff4c94d617500b6ec4a3734c6ba |
5.4052 |
0.3090488 |
137.8723099 |
| 0xcf6566c2276de704ab156f83c89bf9551be4a450 |
5.4044 |
0.3090755 |
137.8637905 |
| 0x59ce4e774d7fd49b965041a9b3bea7e2e107a027 |
5.4016 |
0.2969175 |
132.3720864 |
| 0xb3069e599253926eefcf07916939898dca819981 |
5.3966 |
0.308246 |
137.2953562 |
| 0x15c9afe78f9b7fe1afdbb57bcc83196711bbefd9 |
5.3924 |
0.2696335 |
120.0035629 |
| 0x6099acb926ceaa3b2d260c61dbf24a122e95b1c4 |
5.3919 |
0.3093941 |
137.6867313 |
| 0x04174345baec0e36da6756da78af12ffa95368e7 |
5.3903 |
0.2713241 |
120.7089779 |
| 0xd70be722b9b043fb510c56b31c079ced7bbe7bee |
5.3756 |
0.291598 |
129.3747941 |
| 0xfe5f86f8aefb83d96c5205c1ccc0b140cff79e09 |
5.3746 |
0.3087866 |
136.9754973 |
| 0x7990841bf73a552fcda5db9d68446ac6a5ab1e7c |
5.3718 |
0.308809 |
136.9140421 |
| 0xa8ccf1f24a99a24acff7a577d2913998685190ca |
5.367 |
0.3077691 |
136.3310875 |
| 0xa8529148bb994715321b07bbdf96ca3519931495 |
5.3653 |
0.2718258 |
120.3712663 |
| 0xdfb606dbd40b9db232eafce1bd1caffc78a0db73 |
5.3559 |
0.30882 |
136.513672 |
| 0x4ab4e45f5094d378828b3bae7e6f890dc26158eb |
5.342 |
0.2732276 |
120.4666172 |
| 0x167a9d30b24fd6c6e44e77fbcec36a8d92e75e36 |
5.3412 |
0.2973049 |
131.0626912 |
| 0x7d547666209755fb833f9b37eebea38ebf513abb |
5.3283 |
0.2927427 |
128.7398261 |
| 0xea11015887ab4ed64e5fd9b2a380b0d7eac036b6 |
5.3246 |
0.30882 |
135.715881 |
| 0xbc84b933efb9ea6a031ae44025534a9034122013 |
5.3222 |
0.3042098 |
133.6295928 |
| 0xf8508946af6fe18134eb227c6fefa48dc526eb67 |
5.3201 |
0.2948312 |
129.4587559 |
| 0x62ee415df4c3212f7236549a4011bc2a35d6e851 |
5.3174 |
0.30882 |
135.5323677 |
| 0xc020f3828f3b5f750e340f780380973fe85a0542 |
5.3138 |
0.3084081 |
135.2599194 |
| 0xecbd518c045a22b7c08795b37d5c28627662c056 |
5.303 |
0.3087898 |
135.1521102 |
| 0x3c4b7f7a6b731ebff0207f0ef3191b08c05f93d1 |
5.2943 |
0.308246 |
134.6927331 |
| 0x3ccf1b9a70af6b247d72f7f4de62989d38d1374a |
5.294 |
0.3093941 |
135.1867719 |
| 0x30bc55cd5645c3c3bd6958a0dd401d24a3e6c7cf |
5.2938 |
0.3088201 |
134.9308421 |
| 0x7c7b2e4d74419ab7104ba394d58310803ee6a31c |
5.2928 |
0.3087448 |
134.8725055 |
| 0xbaa72b6a59d4395e1e610005c1c507c7dc16ca39 |
5.2753 |
0.308787 |
134.4449237 |
| 0x59e0d59a31a037bdf3ac38a77a7ec45d5c51028f |
5.2722 |
0.2717323 |
118.2418736 |
| 0x74852d7f2b6cd9fefe4e2da996863337d3e7fea7 |
5.2583 |
0.3088176 |
134.0249228 |
| 0xe87f168a266e7dabc051ec39c2ab4f691e6bac85 |
5.2507 |
0.3087898 |
133.8191933 |
| 0x2bf30735f3e75937808eece8883cdc3e74107f56 |
5.2507 |
0.2713241 |
117.5828125 |
| 0xc01214afd9ed41daa045adb00d20d9cfb1e00b66 |
5.2507 |
0.3075813 |
133.2954371 |
| 0x5d03782725982a743e7afba4a464751d68e127a1 |
5.2494 |
0.288639 |
125.0555237 |
| 0x828c3e780844673a9c142168120709ab67df2e08 |
5.245 |
0.2609535 |
112.9657527 |
| 0xf519765f1ccf2d2522d316d6a5d1771e8972233a |
5.2407 |
0.2008633 |
86.8816611 |
| 0xe5bf793facace70603c2d28713036392a82ac37f |
5.2355 |
0.2716217 |
117.371015 |
| 0xbd9016d269ef5809829a588a42f78f01ba322f3d |
5.2293 |
0.2720733 |
117.4269098 |
| 0x19c4883b60a02074543c8021dad313a27ff3585f |
5.229 |
0.1933713 |
83.4543387 |
| 0x0cc9967c3d48d5ddff289267286b25f719a5e031 |
5.229 |
0.1933713 |
83.4543387 |
| 0x24c0fc81be4c61f99874399d872ff275bba81cc3 |
5.229 |
0.2717323 |
117.2730085 |
| 0xa25260eb0bfd4d38daf65edb909530e8e075b800 |
5.2272 |
0.2732279 |
117.877908 |
| 0xfdd580dd311d6585cb7a39e9bba1bf8969ddd6b6 |
5.2272 |
0.30882 |
133.2333084 |
| 0x5be579250f5a9d711f0aced27ea91afebc941d63 |
5.225 |
0.3066882 |
132.2578869 |
| 0xd984b81f72fb0c8a061d6a4019c6c5201ad9ceec |
5.2124 |
0.2713241 |
116.7251337 |
| 0x4e334a21ddb57247c2fb6d5c3929095a0aa621d7 |
5.2025 |
0.3087964 |
132.5935907 |
| 0xfa9b9fdfaae9bdbab29636060293df2b65409088 |
5.1843 |
0.2963904 |
126.8213722 |
| 0xeb80646a66d271aa323e51335fb474f90286cc6e |
5.1825 |
0.305097 |
130.5014771 |
| 0x808623b13d6efb97ace7ee6f4666c6717adc0092 |
5.1825 |
0.2859288 |
122.3025328 |
| 0xa2d852420ac6fd37bc132685f3a594a09c9867a3 |
5.1719 |
0.3075364 |
131.275874 |
| 0xb01cd4f675c8f727aca5a41d37f5450ab20e4dc1 |
5.1552 |
0.3090613 |
131.5007746 |
| 0x9c35739128867bfb69fdfc6df6386ee6c4c4cced |
5.1505 |
0.3076719 |
130.7902684 |
| 0x2f6c8752826813e850ccf8f78eaf695df34ffa6b |
5.1497 |
0.3048016 |
129.5499732 |
| 0x8d074c2e03f537c68706d838a117e2d416dd01b4 |
5.1472 |
0.3093941 |
131.4381096 |
| 0x92390924296c095dd374c539c2761e69741b937e |
5.1445 |
0.2736152 |
116.177377 |
| 0xad82cc36ba47c59051403d1f4c20960e9d2fa0e2 |
5.1445 |
0.2251794 |
95.6114796 |
| 0x784a0e6273dde0947d008e35763b4f22c559f79e |
5.1319 |
0.3093941 |
131.0474112 |
| 0x61c8bd5a962f97dafc655ce2fb6a91219a944c73 |
5.1302 |
0.3088278 |
130.7642282 |
| 0x023034ab2aee1de8275fe3299be4a0b47dc9fb14 |
5.1161 |
0.3041796 |
128.4420813 |
| 0x3b522e4358de5b85b32cb59e84f12e6e84c94b1f |
5.0973 |
0.3080831 |
129.6123349 |
| 0x34f864a7051868bd8dfc8292f68b8a574c32367d |
5.0968 |
0.308508 |
129.7783435 |
| 0x4b8b8601a4b5d280254c3610af2a44fcf5c12a9c |
5.084 |
0.3087867 |
129.5693517 |
| 0x052b3a2dba295749fe6dc8c0a9facf7bdb1d55fc |
5.0777 |
0.3075812 |
128.9036226 |
| 0xf9a513ed8b0ca264f8e8fa6bf1bee66c0f36e418 |
5.0762 |
0.3081855 |
129.1187174 |
| 0x0891ce1371ec8411c6216ab6c976b70717a87269 |
5.0707 |
0.3083298 |
129.0391796 |
| 0x0de9bde537c4d39ea4411529cb854deb71ee2b75 |
5.0468 |
0.3087898 |
128.6226006 |
| 0x58b5336e368b930ac5111cb5ef63ef5bcfa7242f |
5.0463 |
0.2717323 |
113.1755169 |
| 0x370de685ee9d74aa5ab4e93eb0c04df40d587ae2 |
5.0409 |
0.3027975 |
125.9791362 |
| 0xf1c71afb167fdabddda53fb211bb640c12d85aef |
5.0358 |
0.308862 |
128.3722727 |
| 0x8fbcaf55bb01a671d31847ec3bf7f2616f27c7d2 |
5.0343 |
0.3081557 |
128.0405269 |
| 0xb3873616623f16874f0c4757c2e0647cae8a0451 |
5.0049 |
0.2713241 |
112.0784331 |
| 0xf413d05a69570e94a482268a6beb7fff243449a7 |
5.0044 |
0.3079091 |
127.1782133 |
| 0x120e355cccf2fbd06d8f3cc9edbb2f19c256d2f6 |
5.0043 |
0.3087898 |
127.5394498 |
| 0x630066d360448c8cc664574aedb330452443b728 |
5.0036 |
0.2717323 |
112.2178652 |
| 0x04256cf6b796101674643233cf43d629213de261 |
5.0023 |
0.3093941 |
127.7379655 |
| 0x187089b33e5812310ed32a57f53b3fad0383a19d |
5 |
0.290563 |
119.9081195 |
| 0x69a9e35b769a7b8bad41ff5421e5c365632830a7 |
5 |
0.2935752 |
121.1511822 |
| 0x22996b929510142c95fcda8aa59ef2a257057d47 |
5 |
0.2966984 |
122.4400434 |
| 0x17b21a9b0796372fab7953fab12a13a74a50be5c |
4.9824 |
0.30882 |
126.9937296 |
| 0x4b7da8cc08c1998e6613144b6043c551deb6f445 |
4.9773 |
0.2765068 |
113.5893987 |
| 0xd516dbce1f207ab7b0f0b9dc02e30d38621e4e38 |
4.9676 |
0.2755257 |
112.9657974 |
| 0x04305e934df12870bf457dd470d2e536445800c9 |
4.9647 |
0.2732274 |
111.9580731 |
| 0x0352102cd10b340bf189e0090abe4d61ee40f470 |
4.9647 |
0.30882 |
126.5425846 |
| 0x6b74b18716b97216c296fa174905fd46b6dbe244 |
4.9577 |
0.3076719 |
125.8943667 |
| 0x92f225381f5882e9e1e468fd33c560c22bb8a70f |
4.9534 |
0.3067701 |
125.4164953 |
| 0xe05ec2a9d403c981d16aecaa69297cdeadd65d93 |
4.9419 |
0.3093941 |
126.1956003 |
| 0x012efd9feeaa8b7e1edf4af9f5fff4b1d9431a7d |
4.9338 |
0.308817 |
125.7537663 |
| 0x93de57b1a327d6efc31f2ef53bf27bb1daebd069 |
4.8945 |
0.3089115 |
124.7902318 |
| 0xf54f4815f62ccc360963329789d62d3497a121ae |
4.8774 |
0.2556798 |
102.9255271 |
| 0xf3b27f3944893db2cf03bfbd88af20d42b5514f7 |
4.8691 |
0.308246 |
123.8751899 |
| 0xc6d1cab8aa6c6099a4dd7352ebd4b25521f6c79c |
4.868 |
0.2977667 |
119.6368458 |
| 0x293e6926db7181c810ca5b862280295457185a28 |
4.8384 |
0.2696335 |
107.6747349 |
| 0x531a223de47eee3d2520f0a5a664b38d1bf94b81 |
4.8132 |
0.3043823 |
120.918142 |
| 0x47443d1337192bec41aedc3c49db1fc15590055d |
4.812 |
0.2716215 |
107.8767873 |
| 0x2b69be397864dc6651f50c69ebdb5ce4a19eaa21 |
4.76 |
0.2905078 |
114.1308353 |
| 0xad3ed580e5fcc3eb0ac93e3c72dbf113ca600adc |
4.6904 |
0.3088037 |
119.5447731 |
| 0x75b207b6726e092eab2b2c30d8ef393f5917880e |
4.6791 |
0.3074686 |
118.7411568 |
| 0x0ac64043f5be712deb6c0119d7faec1a9439bc4d |
4.6499 |
0.1933713 |
74.2119582 |
| 0x06bfd7de1e77c31278aa3d5c344926b79d1ea529 |
4.6499 |
0.3012296 |
115.6057475 |
| 0x30784b15b4bbaa753565e6560f0642bce6525e33 |
4.6499 |
0.2732277 |
104.8591939 |
| 0x09be51f586bc060aa1a07b0ddd689decccd1bf1f |
4.6355 |
0.3077676 |
117.7491147 |
| 0xc24f54690c2d4afceac2d87b04d55c064e72494c |
4.5904 |
0.2732275 |
103.5173395 |
| 0x929b3776fb37e775f4df7104fc510ba1fa1acb16 |
4.5762 |
0.300783 |
113.6047617 |
| 0x2cf3b1a52b0b2642b7b99a98200089c98fb3a591 |
4.5616 |
0.2986348 |
112.4335155 |
| 0x99003cfcad31e3b95be0f7e8e783b63533a916a3 |
4.4797 |
0.3076719 |
113.7561765 |
| 0xf61771b1808bf37b0d0a02d52b896c9decf2ed9e |
4.4797 |
0.308246 |
113.9684273 |
| 0xbbeb4a1078a534fdb60e21d0ab5dc11531e7daa0 |
4.4571 |
0.3089462 |
113.6510359 |
| 0xe120adfc210eccd020f553ea4328b3fbf89c0e17 |
4.4376 |
0.3087898 |
113.0965473 |
| 0x17020b5ff186924827855c6faad93bb5f151b296 |
4.4374 |
0.3088002 |
113.0952641 |
| 0x8b4616db3dc83ac568841421ebf9b4aa3c3c7650 |
4.4124 |
0.247853 |
90.2624954 |
| 0x814b07e84d40f81fcfe408966375d31829a95218 |
4.3429 |
0.230564 |
82.6436649 |
| 0x27b675f356efb9da3ae0f28c79f109f47a994149 |
4.3364 |
0.30273 |
108.3485142 |
| 0x9d3de9c7771f358face2f94d7f304d7c2b7adf56 |
4.3322 |
0.304634 |
108.9243954 |
| 0x62132534a3e2bd66c033c231cd2e8d63a35b9296 |
4.3241 |
0.3089107 |
110.2470214 |
| 0x4a4487e81b806b7550b46d5e12baf26c4dcb8279 |
4.3241 |
0.3091891 |
110.3463845 |
| 0xd53b48ce0c89a97f1449c0d32520b6c2830bea2d |
4.3173 |
0.2713241 |
96.6804964 |
| 0xa97ca732232cd2acab9038a1943fe2a79fa1ccc8 |
4.3172 |
0.2683474 |
95.6175987 |
| 0x3fc6dd6a8b4bbef7dfe7f770ae0ea37c3b2e2271 |
4.2986 |
0.3076643 |
109.1546681 |
| 0xacd8df3d34b917546f588746487a4f80744f098f |
4.2557 |
0.3081855 |
108.2483977 |
| 0xe0c9df5675c49f08cb04919b3e59c75a487224de |
4.2555 |
0.30882 |
108.4661674 |
| 0x7b9ab9f84acad6b80269f145dc4d304ec509a2ce |
4.2258 |
0.2889859 |
100.7914964 |
| 0xcce3379afb42f8b3e34c1cab29e1a19078fd2c22 |
4.2151 |
0.2969672 |
103.3129027 |
| 0x73b38fcc7a571235e3f479ae69033e9962a6433b |
4.1549 |
0.3065237 |
105.114562 |
| 0x747c29e6d0529a5f174fa26645bcf8ca0c4d358a |
4.1214 |
0.2215371 |
75.3580006 |
| 0xe98d816891c8bffaf365388e00cc7d6662e91cd8 |
4.0482 |
0.3087898 |
103.1723119 |
| 0x8544bfa437f1a0971367d968f717b6a93e781f3e |
4.0295 |
0.3076719 |
102.3239312 |
| 0x31e958d241486226ecc3ba0e63d68e02f4db0ddd |
4.0153 |
0.3088642 |
102.3584717 |
| 0xd4517efcbb48241ff175a82c325dc4216a4185ec |
4.0152 |
0.2713241 |
89.9153484 |
| 0x779af1af892cf4d0edd721f5af807a699a1358be |
3.9993 |
0.3087423 |
101.9103622 |
| 0xa5ad6ea44cf18fd9b0f1de5caeeca624bd49e443 |
3.9939 |
0.3038592 |
100.1631039 |
| 0xa435c91c8d98451c2f28698d1d1e521ea2c9c939 |
3.9773 |
0.3083646 |
101.225759 |
| 0xc66aac8edbe34ab3d5357f47cf643cb77d11fc02 |
3.9773 |
0.1991735 |
65.3819816 |
| 0xdf9705571338a78f1fb8d55623621007e5a4515e |
3.9679 |
0.308246 |
100.94768 |
| 0xa41a5a093702cf0096389c96586b7d353b97a8df |
3.9553 |
0.3087386 |
100.7879501 |
| 0x07710e8c175fe0ae82e11cade4968eefd95b884a |
3.9407 |
0.2732273 |
88.8660102 |
| 0x814df9e79b27e23143207f47fa09e30260464ec1 |
3.9093 |
0.3075813 |
99.242361 |
| 0x3ac3d81c28c8c093587f1959043911c168fb8569 |
3.8768 |
0.3093941 |
98.9973701 |
| 0x5b3cec6a5e219674d4485be572cd3faae338bfc6 |
3.8731 |
0.3078848 |
98.42041 |
| 0x73870a3be814ba8caafb021c1e77be99b4a63b4f |
3.8664 |
0.30824 |
98.3634938 |
| 0x592064e0468af50545e7b8e7f61a0bc24b45c3c4 |
3.8621 |
0.2732276 |
87.0936054 |
| 0xae662b081d00df31ebfab162f0954e1973eb9adf |
3.8612 |
0.3090358 |
98.4848242 |
| 0x34282c192fc602d3b323efa5d41090ef636ec06e |
3.8581 |
0.3084273 |
98.2119737 |
| 0xc7d586644759b057e7c98d2bf4bf60883e47db6b |
3.8579 |
0.3093941 |
98.5147426 |
| 0x24601188b00c2131ff6f77e2694932a8281e69d7 |
3.8356 |
0.3087898 |
97.7539946 |
| 0x3d432027c11f17bfd03428ebe0351cb68125226d |
3.825 |
0.2993728 |
94.5109262 |
| 0xc78d02e2c6bfdccbbf0087057de9bb0fd1a9a456 |
3.8111 |
0.3093941 |
97.319665 |
| 0x00af811774d4a34fc40a1e6c0911045df0d93a12 |
3.792 |
0.30882 |
96.6522601 |
| 0xe571ae7bcdfd6ea59904fd36564d735b9da5ffb0 |
3.7768 |
0.3021001 |
94.170112 |
| 0x0fb1110da2545ff09df2e39e97f8a09e72a9e038 |
3.7722 |
0.3091854 |
96.2613286 |
| 0x2a18ae61a1830fe92e4921fefad1ac415d4d07cf |
3.7659 |
0.3087867 |
95.9766359 |
| 0x73ca1f3ef3f7e2af8ee8df6d0ef8441a398744e7 |
3.7397 |
0.2732278 |
84.3334453 |
| 0xd591f61f0250cb29c74956b0caf8090508041f1d |
3.735 |
0.2897127 |
89.3092487 |
| 0xfc5a28817a482fb8918c602208eba02bb1c07aa5 |
3.72 |
0.2721433 |
83.5562139 |
| 0x9dbbf9af9cd35e36db5870826d89ee77590e984f |
3.7199 |
0.1933713 |
59.3692474 |
| 0x02d55926475067d1d7bad79e4113a1455ac3a619 |
3.7058 |
0.3087898 |
94.4459151 |
| 0x56c2cb50753a884ca449f59ec17958421cb6263d |
3.7015 |
0.3087749 |
94.3317667 |
| 0xdf951936ca4d4817a67c7b13541a26b35116d21a |
3.6747 |
0.3087866 |
93.6523376 |
| 0x76f980cfe17d4ff3e3f9ddce2129c17e55a1091d |
3.6747 |
0.2926421 |
88.7558518 |
| 0x973ce57f39dc086f976f83f2b2291af5590ec848 |
3.6747 |
0.3093941 |
93.8365755 |
| 0x0bd49029735d7ca4a65dc2f45c73e44f9348fc66 |
3.6723 |
0.2938941 |
89.0773481 |
| 0x9f8701f866ecb0438320c5d8960d3d54143db25b |
3.6369 |
0.3087867 |
92.6889786 |
| 0xd164572b07a7a022facd4b0a63a72c9280ad78e2 |
3.627 |
0.2730199 |
81.729737 |
| 0x1ca15634bf3449bdb8958e42af07a811a18bc847 |
3.5978 |
0.2809862 |
83.4372903 |
| 0x3c2a49e9d86b671801ecebbf5ed328ae2b2782cb |
3.5978 |
0.2732278 |
81.1334654 |
| 0x85214a191345cd1baa815ef33141330e9ec443ab |
3.5913 |
0.3065287 |
90.8575637 |
| 0x5f3582b06b6697fd64e791ab7ace882fe66bc835 |
3.5901 |
0.304808 |
90.3173337 |
| 0xc28396b745db69c5de551cea90af050126981bac |
3.5651 |
0.3075812 |
90.504422 |
| 0x939f281d10ed47257fdfce6ad929d46283f832c9 |
3.5614 |
0.2732279 |
80.3126762 |
| 0xfcdbb57e88251388eb78129a11eb173d477418c2 |
3.5462 |
0.2732275 |
79.9697777 |
| 0x9ee8e4fa81670cc2280549088939d7b6ee654941 |
3.5462 |
0.30882 |
90.3871965 |
| 0x8f34beb69480fa19d8e401fb3c6e3828728ecf4d |
3.5462 |
0.2732275 |
79.9697777 |
| 0x89faa2e1306484d47ec22342fd5b3db6ba8b714d |
3.5462 |
0.299363 |
87.6192416 |
| 0x4bf92605548f9cf02e0345a7857cab1116ffe091 |
3.543 |
0.2788907 |
81.5536641 |
| 0x6674ac1f631910fb851b4949b3b60626b17c3800 |
3.5365 |
0.2753331 |
80.3656152 |
| 0x30ea1d7618c84272c679f2962dd8f7980c999de0 |
3.5069 |
0.2776584 |
80.366027 |
| 0x5d454c8a011b7a9e739dae8435eee7a2d0920413 |
3.4998 |
0.2723486 |
78.6695435 |
| 0x4159dea474e626170b60784b6ceff0a54de2d1a8 |
3.4996 |
0.3070813 |
88.6972055 |
| 0x752ea9232eaaf68f516a54aa3f35aef608a1a132 |
3.4991 |
0.3047414 |
88.0087782 |
| 0x4bfd241e1876df3956625bd11903fa4c085147be |
3.487 |
0.2273007 |
65.4170487 |
| 0x150cc078b61e1b885d263be12666cc7069bbe095 |
3.4759 |
0.3082615 |
88.4351183 |
| 0x20d6702447969489361f4a924f14a19cb1758248 |
3.4681 |
0.2942461 |
84.2249052 |
| 0x904de49b43b8786e6a21e02d3a8ef045bf6a92a9 |
3.44 |
0.2732276 |
77.5749111 |
| 0x81737de19b43bc32508f393d872eed1190dd13a3 |
3.4337 |
0.2709879 |
76.7980851 |
| 0x8e19969e14cb17bc4fe528073cb3b1683cd74740 |
3.4292 |
0.308246 |
87.242572 |
| 0xc41e5e7804cf89755ece46f60346280a9a932239 |
3.4292 |
0.2870056 |
81.2309293 |
| 0x3f56a18c2c7e49f7569393cb705fdd7537209c00 |
3.4292 |
0.3070978 |
86.9175964 |
| 0xb1a2377178d8ab99d78250d831a1edf5d00b290e |
3.4292 |
0.2385846 |
67.5263735 |
| 0xfc27b375faf1fbd3f3462044cf810082f042a45b |
3.4292 |
0.2938944 |
83.1806519 |
| 0x60702925f9966df283d10509ef36ffbaae1f4ca5 |
3.4292 |
0.3084272 |
87.2938735 |
| 0x2cb1b978c9dc9e16dfb8ea0c47e2a603842ca645 |
3.4292 |
0.30882 |
87.405047 |
| 0x1e22968fcd63bf083f067c8619c441a1b8e8f1bf |
3.4292 |
0.308246 |
87.242572 |
| 0xf9a52622d086cdc56b70b01e99b9ba6f23cea624 |
3.4292 |
0.2751309 |
77.8700416 |
| 0xa002c4ffc3b3646bfe5cec4d523163b2af120aba |
3.4254 |
0.273228 |
77.2457604 |
| 0xa34ca8398168f2d692150d1bdd83a2ba545d24e7 |
3.4098 |
0.3079297 |
86.6600131 |
| 0x90915b459b1d80ff1ad614879bd96665e756f602 |
3.3975 |
0.3093941 |
86.7580388 |
| 0xf8a280c1f043f418004125ead0027814a5de5e34 |
3.3852 |
0.3093941 |
86.4439479 |
| 0x961088b76a515d437d9e3e1fc9d24bd295ff3b67 |
3.3692 |
0.2745634 |
76.3497491 |
| 0x8cbefb17547ffb31acf21255b32e00ec11f011b0 |
3.364 |
0.3087672 |
85.7285261 |
| 0x54db737c7b9c72e3dc6a8ac4969a26f27d9a3b91 |
3.3523 |
0.2549688 |
70.5453139 |
| 0x78b30621e4f6603f3bff93974874f5b7bf91a005 |
3.3388 |
0.3081855 |
84.9260429 |
| 0x0afea156b28fb8f0f51d131312f5cda6cb95f536 |
3.3335 |
0.3070979 |
84.4919719 |
| 0x066a516109af8fcc6bdc37ad0e93968dd27c5edc |
3.3182 |
0.275017 |
75.3182636 |
| 0x68b4d26e3bfe87245b6c1114298fe29b5d956c6c |
3.3144 |
0.2767356 |
75.7021504 |
| 0x65c5ae767dec7462a306f8d8c4948e7c44edb69f |
3.3144 |
0.2732274 |
74.742459 |
| 0x081b27df79a6c295d523a5af8c273d8a9b888b98 |
3.3144 |
0.2732274 |
74.742459 |
| 0x24c85830af787a6d243fb45c1ec5a57612bc6623 |
3.3108 |
0.2717048 |
74.2451995 |
| 0x1659d7dc0ba538b8323da7495fa19b4b5a0fe816 |
3.3099 |
0.3079839 |
84.1358521 |
| 0xfe791b87f607ae6be8449e64d393c91be46a1245 |
3.2962 |
0.252242 |
68.6229083 |
| 0xc1b8e82de398e485c2a1b0c88f889dc2fa470845 |
3.2852 |
0.308246 |
83.5790558 |
| 0xda2e1969d7e314f248ca373fdad48b1fb0e2d1b5 |
3.2852 |
0.308246 |
83.5790558 |
| 0xd8fd8d35151c4dbafadda313da4ec0dee4a4633d |
3.2851 |
0.306977 |
83.2324354 |
| 0x9692f158e9b772d1722236f6844b6a0cdc75c2e0 |
3.2577 |
0.2960998 |
79.6136388 |
| 0xa63d200635f8a2853e8c43b506910b5663200255 |
3.2408 |
0.2971513 |
79.4818675 |
| 0x4fd87fa2a70c2141876c3d9d29ab5ab99e0d6be2 |
3.2234 |
0.307391 |
81.7793244 |
| 0x39fd7088530491af658a3337b338627c35044e74 |
3.2047 |
0.3017873 |
79.8227231 |
| 0x48a8250b961b880755d37b1ddd1d0d59ddae80ec |
3.2043 |
0.2800167 |
74.0551681 |
| 0xc11ff87965a59a569f104149ff74180f15498ce9 |
3.1916 |
0.3088201 |
81.3489879 |
| 0x40b852d82bbbade81ba04ef155b9fe02ac479cde |
3.1827 |
0.3087898 |
81.1142018 |
| 0x594bf8496a39c5e5d5f0ab1ec00fd5004923bc31 |
3.1785 |
0.3089896 |
81.0595838 |
| 0xebc1336b4ffd5beff67f84176d8ef45f7d7ef1ef |
3.1566 |
0.3088191 |
80.4566473 |
| 0x3b66fdb8644939050095808f37bbaca31533224f |
3.1521 |
0.30882 |
80.3421925 |
| 0xf67d5f429198f6720cdbbe0dc09d54767b252dc5 |
3.1465 |
0.2713241 |
70.4619042 |
| 0x39ac0cd334223b07496f4a52533719792676e72c |
3.1419 |
0.3081792 |
79.9160375 |
| 0xeca97595b3f6feb638c6b3444d408b40615e8c86 |
3.1209 |
0.3081856 |
79.3835162 |
| 0x9ccfef8c677db9dd434b5cea72720bfd502a6a47 |
3.114 |
0.2732276 |
70.2233324 |
| 0x7e77bd0e63ab0b9b0a1935df2fdf8fbb85a228c0 |
3.114 |
0.2273019 |
58.4197863 |
| 0x42be42552923f70231d4b9b4b9ce45648c1d2edd |
3.114 |
0.2732276 |
70.2233324 |
| 0x4f217324694b8016ba7d5d9b23fd57294454b4c9 |
3.114 |
0.3089107 |
79.3943785 |
| 0xd4d7ce03bd6a29d495173501abf217ba0dcf3c98 |
3.114 |
0.30882 |
79.3710834 |
| 0xc3bf5e6585542fb0ddcb64defa9c6d9b9e3c925d |
3.1073 |
0.3053543 |
78.311483 |
| 0x38b9f1298b77f24acafa45958d2ee4f9d5c4c837 |
3.1013 |
0.2713241 |
69.4497079 |
| 0xd8967c23b6b6c9266348f0a998b8d0c2f8b14d51 |
3.0932 |
0.309046 |
78.8986032 |
| 0x67e95d2dde29d7635f4b39d592c8315918952869 |
3.0912 |
0.272848 |
69.6123266 |
| 0x6a4966ca98641fe11001fc688220ca40845a12d2 |
3.0887 |
0.3093941 |
78.8725694 |
| 0xf1f6c4d5597d114a87b23568e50583e5096f0881 |
3.0887 |
0.3093941 |
78.8725694 |
| 0x205e220f4331015e1e72217e5887d84b8db587a3 |
3.0886 |
0.30882 |
78.7236731 |
| 0xb8b1ff851e120451675457941e473f694f66d809 |
3.0863 |
0.285827 |
72.8080803 |
| 0x6274afb77acaa22d1fc758a162db9fde2de08bec |
3.0863 |
0.285827 |
72.8080803 |
| 0x2e1f7d8082fc91e880dfa63f6c42737d580cb227 |
3.0836 |
0.2736156 |
69.6365282 |
| 0xad1d18c01939464cd8b7dca54ca81b990b1463a9 |
3.0603 |
0.2732275 |
69.0123076 |
| 0x0aba973ba5fac4fc20c3ad7047fbc992611583d4 |
3.0603 |
0.2273015 |
57.4122503 |
| 0x904054db6d430bb62b2b2b7403e15bb1507b77f9 |
3.0603 |
0.3081855 |
77.8420895 |
| 0x784c0c920ed8ec46e0c6ff2d04f3ffa14bfd3a44 |
3.0603 |
0.3087898 |
77.9947204 |
| 0xfff9619cf4d7f254cff6d6e2aeea100591a80a74 |
3.0602 |
0.308246 |
77.8548063 |
| 0xf70d9dbe67f28d27d5854018671dabae45666429 |
3.0462 |
0.308246 |
77.4986323 |
| 0x4884f2370373b1234ce25892a8d41f598a8e9822 |
3.0449 |
0.3088171 |
77.6091036 |
| 0xd7fb9fd4ba3f008af236563d43d7ae3cb1b785e8 |
3.0276 |
0.3035543 |
75.8530577 |
| 0xf15e9fae1f0a2157c31156f7c307cb3769b53889 |
3.026 |
0.3081856 |
76.9696317 |
| 0xdfa2c4fc1622c17415069e9b525abfbd4929fcc4 |
3.0202 |
0.3034946 |
75.6527769 |
| 0x8a41988a2ecb0684f0ab53219c6865a3ea9de853 |
3.0128 |
0.3022034 |
75.1463531 |
| 0x6f0eb4ddcf5d6114d5a975eb73536f0d388711c2 |
3.0075 |
0.2839079 |
70.4727665 |
| 0x43d6ae04ba29cdc7863cbfeebf8ceacd58f8312e |
3.0056 |
0.2915974 |
72.3357598 |
| 0x4785f21860041e32474aa68405b91fc0042b8b75 |
3 |
0.306135 |
75.8005783 |
| 0xd663e34a534d023008dc7d396605657188040e90 |
2.9975 |
0.273908 |
67.7644825 |
| 0xb46c4044c0aa51456a3d5c7093d4ebac05e78a04 |
2.9887 |
0.3083278 |
76.0559496 |
| 0x07a1d90c29b23401f6b43d290b45d7d86bbaa793 |
2.9877 |
0.2987915 |
73.6789644 |
| 0x4da56b01d3767638c58c9e5f06517a39cf2e440e |
2.9865 |
0.3093941 |
76.2628059 |
| 0xdb81f550a3cff9a28f51ed3c92fa7f44b72082a5 |
2.9865 |
0.3087898 |
76.1138553 |
| 0x7d761612d6baf6a3e73d53877d4dd5142246e6b3 |
2.9865 |
0.3087898 |
76.1138553 |
| 0xca5b32d330a81ab5d84565467baa209c4103d7ea |
2.9864 |
0.308246 |
75.9772545 |
| 0x124c7520429f8139997f69b629475ae9b1d726f2 |
2.9864 |
0.2732274 |
67.345784 |
| 0x50c75f92007b31a1b11008c262149d90cf18cb72 |
2.9864 |
0.2732274 |
67.345784 |
| 0xa85c363db5cc934d5fa5e77e974aa5cf9475ede9 |
2.9864 |
0.2732274 |
67.345784 |
| 0x12b6780281688131b39e26b84fc30865c941dc07 |
2.9864 |
0.2732274 |
67.345784 |
| 0xccaaf958c551807b38c202018897168c701d8f6a |
2.9864 |
0.308246 |
75.9772545 |
| 0x4a8e858c0cf7717b570de4a26029e5618776196f |
2.9864 |
0.2870052 |
70.7417707 |
| 0x7753bdb62e260c3554c14abf11a9585601973f87 |
2.9864 |
0.308246 |
75.9772545 |
| 0x93c71908a4af260cd080533e2947b0fd5a7cc5dc |
2.9864 |
0.30882 |
76.1187518 |
| 0x5afc03363e01c53b88a40239d63b8f61ae45702f |
2.9864 |
0.2732274 |
67.345784 |
| 0xc7f1c7a603c66ceb11addab7a067b752cf5a110c |
2.9864 |
0.30882 |
76.1187518 |
| 0x1128b6b04008bb354c74a246e6922bef4c383531 |
2.9864 |
0.2732274 |
67.345784 |
| 0x719a962ea2330c0a92730f0611446aa198e07baf |
2.9779 |
0.2967041 |
72.9242397 |
| 0x27a3ae9705f6d941e4483b3206473f30a18aed2e |
2.9721 |
0.2915047 |
71.5067768 |
| 0x24361d98dade35cf9c0bf154c576164f419494ef |
2.9709 |
0.2732271 |
66.9961663 |
| 0xf4e778e56895362bf829dd2fdb339080d14817b9 |
2.9678 |
0.3084273 |
75.5484565 |
| 0xc1c28e6270a4aebc03c5677b7e7372fddad5b3ba |
2.9678 |
0.276736 |
67.7857539 |
| 0x99b279cd45c45550968c0d35d0945a7e1329dad4 |
2.9678 |
0.3093941 |
75.7852856 |
| 0x4763000409b99fa043098596dc57a79005e703ac |
2.9678 |
0.3088838 |
75.6602908 |
| 0xb235940f122b44ae654a41188801dee48a5463bf |
2.9678 |
0.2751314 |
67.3927189 |
| 0x3c0d3b28fef414f884eb2555758995394f262675 |
2.9678 |
0.2732277 |
66.9264311 |
| 0x641c4e11c021e47940f39b95a5c9ceb130c85d6c |
2.9678 |
0.2732277 |
66.9264311 |
| 0xe664549ecff3177fa68ba8ad311e826eef03fba2 |
2.9678 |
0.2713241 |
66.4601434 |
| 0x1b126851b975a7383bdc3cecf95acc8a6df6977e |
2.9678 |
0.2732277 |
66.9264311 |
| 0xd0c6cd140ed3832e2567ce93e80801c7d97ddf02 |
2.9678 |
0.308246 |
75.5040529 |
| 0x1e74ccb4458362f6635c5007cb7b41cc101127dc |
2.9678 |
0.290057 |
71.0487052 |
| 0x5c4b9a8c815b07a996ff740267e4dbf462cf0d4d |
2.9678 |
0.2732277 |
66.9264311 |
| 0x9cfb17b4179ff9b23375f28cfb6ce4230fb1bda3 |
2.9618 |
0.30146 |
73.6925527 |
| 0x12c4fbaf2f41b93cd5e7e671635747ed46883ea6 |
2.9509 |
0.2833864 |
69.0194704 |
| 0x404d76baf1dcf7cdbd49f149a128c69d8ebfc10c |
2.9342 |
0.3081855 |
74.6345956 |
| 0xfc0810d9a50428f7f12f9032c9e1ce73ae0449ed |
2.9332 |
0.3085146 |
74.6888274 |
| 0xffdf137a172d802f72321bb5c0196dd49fe9268f |
2.9073 |
0.2803884 |
67.2803324 |
| 0xae5076b2e3aff4c0cf47d31e85d7cad47a0d8588 |
2.9059 |
0.2229813 |
53.4795001 |
| 0x87de0e75af8669d3673e8d276e823adb3168d872 |
2.9051 |
0.3083735 |
73.9394843 |
| 0x362b7e0599e950b921ca9d86336ca409208ffdec |
2.9051 |
0.1991742 |
47.7565019 |
| 0x3e6630cbef0b4427b7209a8536f150566e0e60d2 |
2.8999 |
0.1955758 |
46.8097604 |
| 0x4c265b66caacffba6ef1a01a007f1dd5c7e2dbd0 |
2.8968 |
0.2713241 |
64.8701858 |
| 0xdff8dfbc3f78cf7851dca318bd0b93b68795d6f3 |
2.8968 |
0.3081731 |
73.6803115 |
| 0x1c5218d97afa1bba5cebe9d858c835f70a3ab022 |
2.8871 |
0.3052618 |
72.7398741 |
| 0x45ba78b645c59e16b11d0bd19fabb1c66800b297 |
2.8867 |
0.2732272 |
65.0974166 |
| 0xbdf0c858f8db766562ff79e59ba04d58fad952be |
2.8862 |
0.3081855 |
73.413663 |
| 0xf4c7a44da126a42e6de3905e562e0c3bbcfcb696 |
2.8805 |
0.3070978 |
73.0100785 |
| 0x55c9a5b941790c0939c7e189c45b45e10ff31dcd |
2.8782 |
0.2732275 |
64.9058115 |
| 0xd049307685b7b3a6aa2e6c34fb0ad0128ac1bc45 |
2.8674 |
0.3081855 |
72.9354659 |
| 0x54de892a28b4ddfcab742dd4edebb91c2e4e83cc |
2.85 |
0.3081855 |
72.4928754 |
| 0x7c84bf06d5a2d5d7f5d08045340334c73ac0ee59 |
2.8371 |
0.2713241 |
63.5332821 |
| 0x938ff34c3bf2a1733b6090cee45562749aa8c32c |
2.8371 |
0.3081855 |
72.1647526 |
| 0x7817d830181c6ee05c8a28d9f94be7cf202f2b0c |
2.8369 |
0.30882 |
72.3082257 |
| 0xad920cd7046c3e3c5b562bbf61c60d7a0b5d85cf |
2.8369 |
0.30882 |
72.3082257 |
| 0xea24efecbfd190ecff39462d8b0d318c73020d01 |
2.8194 |
0.3069769 |
71.4332974 |
| 0x179053edb38a668af000953aee6584bcdec830ec |
2.812 |
0.2484936 |
57.6725053 |
| 0xaa3600788b72863ff51c8f0db5f10bb65fbfeab4 |
2.79 |
0.203765 |
46.921518 |
| 0xe59136eff335682362aaec7f40d4d469a05b6a99 |
2.7845 |
0.2676429 |
61.5093556 |
| 0x281ba139840a7497a6ed40a20ac0a4b0a5d604f0 |
2.7468 |
0.3048015 |
69.1006808 |
| 0x951d71a03538a410f4da2dbbcd13a0cecf6f9b58 |
2.7443 |
0.3048446 |
69.0475471 |
| 0x46354bcf55f96101342cfc9d7c829688475e32c2 |
2.7434 |
0.308246 |
69.7950739 |
| 0x988c0e88623ed00c939044697b38052f383201a3 |
2.6952 |
0.2732282 |
60.7791644 |
| 0xcf247f4853c1354fe0994f710a86e7c662c59d60 |
2.6515 |
0.273228 |
59.7936468 |
| 0xb9ea10d8729018acc3a8c658d3843ccb1a907e0b |
2.6514 |
0.3058221 |
66.9240563 |
| 0x85d07590d6a150090a6fce0646c16d583482f1cd |
2.6489 |
0.2696335 |
58.9491572 |
| 0x2258ef5c17f1c1c4d7aa511febaa9d6ddf073c63 |
2.6432 |
0.3081855 |
67.2326921 |
| 0x5f5f7fc66a5996bc43c9cacb0efc6735706033f6 |
2.6352 |
0.288298 |
62.7037374 |
| 0x5f24f798ab2d24fc73e905e5f9688009cd2994c7 |
2.6021 |
0.3048014 |
65.4604756 |
| 0x213c6aed9834dd9e0e43f36fdf33f51f9a094192 |
2.5605 |
0.272078 |
57.4984785 |
| 0x9e455c19f84831867f8d5c08e7c22c6e9006d7f7 |
2.5184 |
0.3093941 |
64.3094761 |
| 0x9e7d109530bbfd53496b9d406b861e06457b0a81 |
2.5166 |
0.3087898 |
64.1379965 |
| 0xe36b9f8dad2120699996de9479dac5e6b075104c |
2.49 |
0.2894087 |
59.4770054 |
| 0x0e4fd07aa8f8e8c616ff4ef909d42de92407543b |
2.4824 |
0.2713241 |
55.590223 |
| 0x7e19f07a79f7efa7c4793289bf750cab8f5d8231 |
2.462 |
0.2736154 |
55.598969 |
| 0x3818ca0c7bf45199354268a9620f167e26521c7d |
2.4423 |
0.30882 |
62.2504793 |
| 0x606287e4fbf1d4fda67a3a0a6f822ee331c2fd75 |
2.4414 |
0.2954115 |
59.5257055 |
| 0xf78f53c8ef82072c3bf2e417e26fe506e89c316c |
2.423 |
0.3081296 |
61.6204653 |
| 0x31f665f338a1ec8efcddb039d851593930ad4f5b |
2.4107 |
0.3084632 |
61.3740411 |
| 0x3fa515df9e7a82ff12990ce279c707f95d2fcc7c |
2.4004 |
0.2732273 |
54.1309866 |
| 0xcc4278284c155c9ad59f86dbb7547aec8d5b4a62 |
2.3892 |
0.2967648 |
58.5198325 |
| 0xe5077b472915a79629df05e1cfc6d4c87de2cbe2 |
2.3892 |
0.2783946 |
54.8973684 |
| 0xae143d5c19f0b5983c8b8639ab859a2916269efa |
2.3773 |
0.3084471 |
60.5205534 |
| 0x3ba0578af54fe01b9758b65a2780769309b101b2 |
2.3742 |
0.3064935 |
60.0588142 |
| 0x5316b787ab0391bdcc7939457929915d050062d4 |
2.3701 |
0.2721564 |
53.2382023 |
| 0x14be80675270a2b469842909c6d2fc129f05f451 |
2.3439 |
0.2779917 |
53.77856 |
| 0xf9e37a804db126ff2b3fb52f3b42ad7a3aaa4452 |
2.3432 |
0.2967041 |
57.3813998 |
| 0x0fe843a32f63875d6262e583f47c3a64b664795a |
2.3405 |
0.3090462 |
59.6994386 |
| 0x5c25a74ece5f94adaf256fcff8a7bdde89816d1b |
2.3339 |
0.2956011 |
56.9411905 |
| 0x96e7976356b96ac57a380ebc9f921fe5e90a0e91 |
2.32 |
0.3078594 |
58.9492976 |
| 0x3847ca178e113e9388681cd391accc6b32995242 |
2.317 |
0.3055267 |
58.4269746 |
| 0x0f7318e9d1eafe53c3bfd7ee774ce33020cf53f3 |
2.316 |
0.2930784 |
56.0222544 |
| 0x9946785a396ef1dcc3640b8cfaa25975d2536296 |
2.28 |
0.308817 |
58.1131359 |
| 0xb1c9b8175a3dd32ba6a4cf99ebfc5cb642aed25c |
2.2596 |
0.308817 |
57.5931782 |
| 0x051762315159646c7cb623addbc2ccc527889ee0 |
2.2193 |
0.229024 |
41.950308 |
| 0xc3fc21ce1071e2f156d6065f65cd8aba0082bb06 |
2.2175 |
0.30821 |
56.4090139 |
| 0x98d5a312d54e546cf530256e385480dde97646a7 |
2.2126 |
0.2722274 |
49.713349 |
| 0xeaf16eb1310b503f951ba57775d8fcc9f460783a |
2.2065 |
0.3086554 |
56.2103227 |
| 0x9b9f5f2b65b829408c00894966fd9ed98949fb2d |
2.2048 |
0.3033196 |
55.1960389 |
| 0x9607b528a8c25052d9d11573886ab5077f0a78d8 |
2.1947 |
0.2960998 |
53.6354028 |
| 0x377663a2b0b371dc0c5ca45394a745a1f44761ee |
2.1801 |
0.2732276 |
49.1630834 |
| 0x1d3356c7c1bf57136e80f340975a6bc493fc0e6b |
2.1789 |
0.309258 |
55.6155832 |
| 0x93ad9911997f08169f14e69dfff16dfc5bd92274 |
2.1766 |
0.2251786 |
40.4523688 |
| 0xa2c54b4e7901a0e7c340084a5cf125df5b6217bf |
2.1621 |
0.285827 |
51.0055234 |
| 0x018923cf7bec398d51d90d41decba688bb89508b |
2.1389 |
0.2991109 |
52.803279 |
| 0xc9dbfa057e0b933acde9f0c222c01729f283184d |
2.1278 |
0.2560058 |
44.9592191 |
| 0x6b31e68df321afb855702df63c9964a540fd2ce9 |
2.1231 |
0.2710244 |
47.4916186 |
| 0x9aecb57447049464eb4a3b7ff5fc54a0f6f24481 |
2.1211 |
0.3063299 |
53.6276463 |
| 0x643ecbf45e98d26998f1f68a7441779d69b830f4 |
2.1043 |
0.3086329 |
53.6028861 |
| 0x4e80613d6250bcc78ec64620bbfa7da7b9265459 |
2.1043 |
0.3091936 |
53.7002543 |
| 0xf78951e62df5a7c87020e3f4894d8745cd37b32d |
2.1025 |
0.2873007 |
49.8552485 |
| 0xcb87ec5c39c6d659dbb75a1dc3321fcaa9e948bd |
2.099 |
0.3087216 |
53.4832315 |
| 0xb8adde7f0a47fec67ee8a9cc159f33aec606a044 |
2.0868 |
0.3086287 |
53.1563759 |
| 0x353c2b72239f4f244a86e47bceeadd123ce0c732 |
2.0775 |
0.2732281 |
46.8494591 |
| 0x2390e4bd1614fec12f587727d1df2bc93119b159 |
2.0775 |
0.3093941 |
53.0507213 |
| 0x3dd1161fc27ccbd1f236ba730ef311e26728f95f |
2.0719 |
0.3013904 |
51.5390535 |
| 0x98888cc6a110f2836a1b182b9fd0becaf145d388 |
2.0708 |
0.3081855 |
52.6730717 |
| 0x8f96ab72ee30fedddcbec3eeeb85c12c691cb79a |
2.0582 |
0.2713254 |
46.0910093 |
| 0xbad9f0ca9faabd16b0162c8f8fd3fb639394be68 |
2.0576 |
0.2876398 |
48.8481594 |
| 0xc40128e8b1c9c8f3707191ba8a49fc844f565388 |
2.0576 |
0.2876398 |
48.8481594 |
| 0xe569ba8857ee48ae7f93d4de0f408067526b0a00 |
2.0575 |
0.2882442 |
48.9484131 |
| 0xf514c2a818621ad0c234503ed131fdaffc5b6f80 |
2.0575 |
0.3093941 |
52.5400044 |
| 0x780b8d7a3299b4aa67a42f498a37abc2efb0ed95 |
2.0575 |
0.2973388 |
50.4928179 |
| 0x4eaaa4dad658af9ef7c531f02b7dc738d78f538a |
2.0575 |
0.3057585 |
51.922621 |
| 0x072067d2df7689d9a191944229dc24c665c056f2 |
2.0574 |
0.3086287 |
52.4074765 |
| 0xfbc56be13c23c18b6864d062e413da3c7e0f74fb |
2.0486 |
0.3081556 |
52.1033318 |
| 0x3e216118a1ad550588bb36a29969155b45bda55d |
2.0351 |
0.3087898 |
51.8665028 |
| 0x024ab28b1f704c46b95a6abe57fa05dd32aa1625 |
2.032 |
0.3087975 |
51.7887909 |
| 0xc3ab2bfd99875629fceb1643ecfcfc99b50bbb1c |
2.0308 |
0.3077021 |
51.5746026 |
| 0xbb2c69953cc7010caa58f381a8eabdca6f861886 |
2.028 |
0.3093941 |
51.7866969 |
| 0x5b191dee6a09918c6b729547dd15ce8eb83a7085 |
2.0152 |
0.3068427 |
51.0354802 |
| 0x58ba15026605bd25d79d1eb2822ded321d7796e1 |
2.0115 |
0.2680823 |
44.5067973 |
| 0x9d68e88aaf9ee8b9d18335e8b29b0b45decfe34d |
2.0085 |
0.3089491 |
51.2149717 |
| 0x0099249b5ff40ff8adfc114023f6702bff8f40f3 |
2.0024 |
0.3091116 |
51.0862806 |
| 0xfedae8c9973ba32da2eebcac4148df5a4a916def |
2 |
0.2489656 |
41.0967531 |
| 0xbb4e936d0f29a515757c518fa883794c4048ef62 |
2 |
0.2938942 |
48.5131195 |
| 0xd483c97638b7bae7e5b5f142af1d1dd9c69ec2d0 |
2 |
0.308817 |
50.9764349 |
| 0x6c965b656c450259a6d4d95a2e68fb4319eecbc0 |
1.9934 |
0.2897037 |
47.6635834 |
| 0x08d41267d3d5baa634ec4e52d6d6b32b76b7c838 |
1.993 |
0.3081855 |
50.6941425 |
| 0xf2c48ec4a8b2275e6ced526b6c9a17ed699ca759 |
1.993 |
0.3081855 |
50.6941425 |
| 0x0534a6af7a3d1997ef931d7235c4f1dcc3a9c895 |
1.9886 |
0.2767353 |
45.4203263 |
| 0x03b8d3fc3059d7a4c5b060449717b6e3aa08a40c |
1.9886 |
0.2767353 |
45.4203263 |
| 0x3ac3331786f0b853759d53e37f57dcf86d800a39 |
1.9886 |
0.2765834 |
45.3953937 |
| 0xbdd338e0238c1b4e2e09566157a13595568755d2 |
1.9886 |
0.273227 |
44.8445185 |
| 0x34dea2a8c64dda1d03bc59b0f226a65940c3f70f |
1.9884 |
0.2531345 |
41.5425739 |
| 0x641bc639ac5e743311522be9007591267b95b443 |
1.9881 |
0.3085079 |
50.6224059 |
| 0x954e28580e05acdab8782091bc99a4ae96c72de7 |
1.9877 |
0.2229813 |
36.5811632 |
| 0x3666ca6938ec1d7627716cae843520081e728c32 |
1.9872 |
0.2717323 |
44.5677801 |
| 0x27963d036cc7910390f8b1f76e27e212477632ad |
1.986 |
0.3087898 |
50.615141 |
| 0x41ec28eceb137789032b2b505a57c1da829934cd |
1.9806 |
0.287005 |
46.9163726 |
| 0x8aac40061e258d6e45fd13e214710abdf356285a |
1.9777 |
0.3093941 |
50.5022438 |
| 0x61adcee0922dea2fc417803a661111554cd5f7c2 |
1.9775 |
0.2868239 |
46.8133801 |
| 0x0b21aca63c60b3b4caead6b05d417f77b404e386 |
1.953 |
0.3087898 |
49.7741019 |
| 0xf45e27f5ae17eba506febf7f84c07d71fbe87b06 |
1.9203 |
0.308246 |
48.8545146 |
| 0xa18d1bf832c6b973476a0a8deaf840cce004f4fc |
1.8883 |
0.3014646 |
46.9835159 |
| 0x24ab3a1c19401d2908189f518b04e1d44dd7eb50 |
1.8829 |
0.308817 |
47.9917605 |
| 0xde4805cd27dbbefe1aec5acf7682dc02d136cce4 |
1.8829 |
0.308817 |
47.9917605 |
| 0xbf8d99e17f5ec3fbc76874bd630f72875c5c137d |
1.8687 |
0.3085181 |
47.5837232 |
| 0xff6b0bc91cebb80eae3232e2658b17195345ef6f |
1.8576 |
0.3093941 |
47.4353887 |
| 0x1a8a6d9a92d43ec8a858b53af7d4eeac86b3e685 |
1.8443 |
0.3041796 |
46.302012 |
| 0x7e27b766d9c2d3e5c45a450a065f2cfcfbbfe631 |
1.8407 |
0.3076978 |
46.7461187 |
| 0x88fd52c4c766eacb16768e98373dbe0c7005e65f |
1.8362 |
0.3082459 |
46.7149171 |
| 0x515f1bccb397be6c0a38160808547cf835ce0ae4 |
1.7988 |
0.2979124 |
44.2292642 |
| 0x80ffe32c46d21203bbca11f2c1e4ae842c760793 |
1.7988 |
0.30882 |
45.8486486 |
| 0xf7cb438968e20bca0f62af26d317f500e932d233 |
1.7988 |
0.30882 |
45.8486486 |
| 0x8ef8c599813e963f36ffa1a99dbdbf6e0f5ceb70 |
1.7826 |
0.2713241 |
39.9190814 |
| 0x1bb548ad5c3ed3b7c7d995ce67bb1f7400bdcc03 |
1.7806 |
0.273227 |
40.1539409 |
| 0x9961d02489bdb014f85db0fd76390eb0fa88e750 |
1.7765 |
0.2976259 |
43.6389424 |
| 0x541cfd983e4804ca02f7f25d2ef669671682d4d7 |
1.767 |
0.2713241 |
39.5697382 |
| 0xbcd236472ebb2bd5c1507a523d8db6a5093e4112 |
1.7344 |
0.30824 |
44.1241554 |
| 0xf980cf31f2263035818230b5555399db761e79f5 |
1.7343 |
0.3085836 |
44.1707998 |
| 0x16d0521e17a5c59cf835227062b2e42d42235fdf |
1.7297 |
0.30882 |
44.0873998 |
| 0xc93f37c0f750cad168e445f3a1e7cc13b93cd297 |
1.7296 |
0.2713241 |
38.7322135 |
| 0xf83f3fa31c55ac262267ff438087d7d52b645ebb |
1.7214 |
0.2732283 |
38.8191216 |
| 0x5c90ee8fe9d306a06b99616af0e0cfd0338cc012 |
1.7146 |
0.2731365 |
38.6527779 |
| 0x0441d6eb0fe8e7bbb5d27d2c825311078d447af0 |
1.7023 |
0.3081855 |
43.2998679 |
| 0x7b9206f601977c143814750a8eff5e227709c68d |
1.6976 |
0.3088263 |
43.2701026 |
| 0xecad91d97ab9ff4bdb79897eb514728b828b1103 |
1.6947 |
0.3091377 |
43.2397278 |
| 0xf7781f6ec1a1ca2c2f2b6a30f443e1efe9c0c6f5 |
1.6749 |
0.2765637 |
38.2315865 |
| 0x9defb747fdc991369f0a93a16dae7def554b7a6e |
1.6455 |
0.3081855 |
41.8550975 |
| 0x5720b052be5f5f0f82ef7eca38cb80b3370ac918 |
1.6425 |
0.2967643 |
40.2304878 |
| 0xf107f51199a41ac18045cb1abe9d3efc53612d61 |
1.6386 |
0.3085875 |
41.7339459 |
| 0xc9bcbebd1065a0114decfd7cb08bd190c6186786 |
1.6354 |
0.307601 |
41.5192916 |
| 0xb6202bf46f93d747f1ce8d74352a9d3b8e2730a2 |
1.6162 |
0.3081856 |
41.1098211 |
| 0x91d0204b30785694d4b4af93f8823abef1510dc8 |
1.5914 |
0.2732284 |
35.8875106 |
| 0x30e2803dc4a9ec782559554eb2c207240f6b9736 |
1.5855 |
0.3081856 |
40.3289317 |
| 0x00dbd0c98861b7ad0fad143f646ef374f4a39f2f |
1.573 |
0.253662 |
32.9323269 |
| 0xeb25eaaee28275831b4f5d031420cccc11f3a207 |
1.557 |
0.30882 |
39.6855433 |
| 0x626158f12ddd02f99abef1fc9e4ea1505fc9f3b6 |
1.557 |
0.30882 |
39.6855433 |
| 0xa615f34b170329507b37c142f8f812b8e1393beb |
1.5529 |
0.3070978 |
39.3602964 |
| 0x341fba0ef5e7d1b30c638c9ffccc3a8a1b87dddc |
1.548 |
0.2966984 |
37.9074376 |
| 0x9183224364e7ab971b3805bf5730497945edd33c |
1.5443 |
0.219264 |
27.9471328 |
| 0x60692ddbbf5c7c6902f931a70103e7c91ac8958b |
1.5443 |
0.3093941 |
39.4350079 |
| 0xc5d53218cec69e7fecaf9fdcfd27e38645cfe2b6 |
1.5301 |
0.2713242 |
34.2646629 |
| 0x280ad4a14fe3fd6668a032ffd96b7fff96ddddbf |
1.5301 |
0.2732275 |
34.5050318 |
| 0xa81fae543b7b336d3a05d17a1a966d96923e9887 |
1.5301 |
0.3093941 |
39.0723989 |
| 0xb6abbfc37d305f3f2201782a0ea00d6fc05c81c7 |
1.5301 |
0.30882 |
38.9998994 |
| 0x3c60c84783020454c16aff48ffb247c9340980cd |
1.5301 |
0.30882 |
38.9998994 |
| 0x39f84aaf54d50708d70c83ac3cc9a78c00d66621 |
1.5301 |
0.30882 |
38.9998994 |
| 0xae908da09e25f27b6c8bb2b25ff1712bc4ce2fdd |
1.5301 |
0.2713242 |
34.2646629 |
| 0x6a47c05e80a3083c54fba622daeabd439139769f |
1.5301 |
0.308246 |
38.9274032 |
| 0x581eeeadd14da757ab8ab106eda2b25e9aa7c7d2 |
1.5227 |
0.3076718 |
38.6669886 |
| 0x9ef53569800e203c20200256cf134abc675bc8e1 |
1.5196 |
0.2602114 |
32.63576 |
| 0xa1c9e423b8830f4d70dd2f5eaf87119e9a52d8b7 |
1.5163 |
0.3083735 |
38.5922803 |
| 0x28248c3fb91971b46fe4a8fe849d48478193db7c |
1.4933 |
0.308246 |
37.991176 |
| 0xc6a26a71156c65357e4971816258b93f5fd387dc |
1.4933 |
0.2950427 |
36.3638723 |
| 0xb80b1423b9cea2ff7d1ae56e4e2fa61a49ced93e |
1.4933 |
0.308246 |
37.991176 |
| 0x87bc972dd3f9b69113db5c44b81b0b02424c3744 |
1.4933 |
0.2732286 |
33.6752892 |
| 0x1eef67f939d55785568926b664f26b8639dd83d2 |
1.4933 |
0.2967649 |
36.5761294 |
| 0x7d7ff0c00ca185eb725a3f0c5a86c4968cf7eec8 |
1.4933 |
0.3088201 |
38.0619263 |
| 0x6f0118af01a543a00a6af3f58fc5a115d21e1455 |
1.4933 |
0.2732286 |
33.6752892 |
| 0x25f969ab173005f1234dc834566901bfd1df5dbc |
1.4932 |
0.3081855 |
37.9811787 |
| 0x5ee2006e03e0bfe49e0b75b573b608eb2b3aa800 |
1.4866 |
0.3075813 |
37.7391596 |
| 0x55b74d42ac254e459c1f297a910f9c7ffd300e00 |
1.4844 |
0.30575 |
37.4589515 |
| 0x988162c50df5ab1d6eb403647750f3b41fcff140 |
1.4839 |
0.2861896 |
35.0506978 |
| 0x90e737f13c808d2a3b8558edb3431508404c0c55 |
1.4839 |
0.2979127 |
36.4864763 |
| 0x27fa9c04d024a968ca29707c96cdcf74195254f2 |
1.4839 |
0.2273022 |
27.838548 |
| 0x86a4cc36b1e0802634889d3106cba3095526b78a |
1.4839 |
0.2732278 |
33.4632172 |
| 0x09de259ba39c8c99a6852c4cd0fd5d231cbb9396 |
1.4839 |
0.2732278 |
33.4632172 |
| 0x5f9b881eba612d7529f1a455f525e6dd8764039a |
1.4839 |
0.2072699 |
25.3851117 |
| 0x2a3da5f42b8bd71f061a9dacbc1ce679adffbdc8 |
1.4755 |
0.3019635 |
36.773247 |
| 0x468851958a8efea32352ce48f3f6700b7f38531f |
1.4729 |
0.3076628 |
37.4012852 |
| 0x0ac1c1c174c0177bd7ec4b1067a2fc4563d39854 |
1.4708 |
0.1991693 |
24.1776588 |
| 0x80556943ffb72344d1bffd90d28750e924c094d2 |
1.4679 |
0.2958598 |
35.8443423 |
| 0x91bf3c7bf154b49aa4858ae0d17e39a6d9ec72d6 |
1.4525 |
0.3088839 |
37.0296429 |
| 0xab0ec712b8b7a9b12b659167aa4b91e1041118e4 |
1.4391 |
0.30882 |
36.6804529 |
| 0x09b0f27549dcaf5d31355628f1f0ea6e1c0c4dae |
1.4391 |
0.2967649 |
35.2485942 |
| 0xc1b442d72b4a082f358c68f3722fa8b98e29e016 |
1.4334 |
0.2713241 |
32.099188 |
| 0x3eabc0be24b1bb616b61d899b7e04f65aa01962f |
1.4186 |
0.2713241 |
31.7677614 |
| 0x9bf8e8569b9b5326efe43a04757698fca85d51cb |
1.4185 |
0.3087898 |
36.1518513 |
| 0xc32f82d6af01e530ee1f0ae4cf22417040373ed9 |
1.4185 |
0.30882 |
36.1553881 |
| 0x4a72bae19e62dcc71504ce5412b00505e18e94a3 |
1.4185 |
0.30882 |
36.1553881 |
| 0xfb53fb29ed29682c911a7317d6743b24ee9864d9 |
1.4185 |
0.2732269 |
31.9882954 |
| 0xf7636f8037841a1e79775f759399b1bde714e2fd |
1.4185 |
0.2732269 |
31.9882954 |
| 0x0c1adad85a343c94b4ab67869048d7c89896c24b |
1.4124 |
0.308817 |
35.9995556 |
| 0x2d24044a8c854d6d0b6164046871b8e32a16c035 |
1.4097 |
0.2713241 |
31.5684574 |
| 0x9d96b1c2bceb6043a4a9a0372df098f92a3d926b |
1.3964 |
0.2696335 |
31.0757687 |
| 0x048b377fbebcaad76bea3bc0bbfe91aff81078e1 |
1.392 |
0.2732276 |
31.3907757 |
| 0x6f2449187dbc51ba2f11dfc9d928f07defb0e0d8 |
1.3717 |
0.308246 |
34.8975369 |
| 0x501ecb2ed1bafeedcb122b321618044c07e6c324 |
1.3717 |
0.29045 |
32.8827938 |
| 0xc8a8e770e766a61e6e027695421e1db191b9df18 |
1.3717 |
0.273228 |
30.9330425 |
| 0xf25d595d2f79b122b0d509d9331b6a3e08964ea0 |
1.3717 |
0.290057 |
32.8383007 |
| 0x7662e754c20a5f8d47f590ca26b65dbba130395f |
1.3717 |
0.285827 |
32.3594079 |
| 0x4852c416378413db83c55e646e15266e79e73bd1 |
1.3717 |
0.2713241 |
30.7174944 |
| 0x5020b38e1b9c7cf26490f1287f7251189bf804bc |
1.3717 |
0.308246 |
34.8975369 |
| 0x4b35907cb789e1b8c79d9a07ae07a87e0166780c |
1.3717 |
0.308246 |
34.8975369 |
| 0x66210015d8c8f8354b0ca771f164bda86747783f |
1.3717 |
0.273228 |
30.9330425 |
| 0x83bbe9cfcc205bb8e53cba0b51d6db9386ce58b5 |
1.3717 |
0.3093941 |
35.0275208 |
| 0x79bdda65c706cbda69c0ad4c8da1d3e91724f48d |
1.3717 |
0.3093941 |
35.0275208 |
| 0xf4182fbed8439874a4adc5ec5cbf6e513543e224 |
1.3716 |
0.2973082 |
33.6567789 |
| 0xf2e724e5a5f7255ea0fd1eec036675f7bd361054 |
1.3712 |
0.2599339 |
29.4172346 |
| 0x199bc5ac41bdab443d067023437ee1a7e5094ab7 |
1.3705 |
0.2736147 |
30.9497142 |
| 0xccc2e6b4a65d9741dc02ef53cbff069fe668ef2c |
1.3671 |
0.3087898 |
34.841872 |
| 0x740909a8e52da6dc7d533c69adc8d02499a7b0d1 |
1.364 |
0.2026102 |
22.8094002 |
| 0xc947b00d5646d2d0167100c06dce3bc638b4253b |
1.3593 |
0.2713241 |
30.4398112 |
| 0x562e1236ad1bd5be28cb78bb8d6adf9b0524d4b0 |
1.358 |
0.3057684 |
34.2713022 |
| 0x401925b73ce7a7996fa4fddc5adbb4a70f46c9bd |
1.3476 |
0.2713241 |
30.1778039 |
| 0x6234ceccfeca398e0a68ca7d18638b9cdad1ea32 |
1.3439 |
0.308246 |
34.1902738 |
| 0x553b818cb2b8e54676edfd6c3993ca0c2de256fe |
1.3373 |
0.2413893 |
26.6431192 |
| 0xcf3b35077e9e8a64654b2c0b67cdef5ce2ae34f0 |
1.3258 |
0.3088838 |
33.7995881 |
| 0x98cbbac87eecad2c7d5a9ea8af089419ee6e8ecb |
1.3258 |
0.2767361 |
30.2818241 |
| 0x7d0c59b979b5c8737bc8df72671a939e1edf7dcd |
1.3258 |
0.3078633 |
33.6879135 |
| 0x4bb2d016b90565612d81a7a4b1b80f49e652cf23 |
1.3258 |
0.3088838 |
33.7995881 |
| 0xe59038e8345c2b801ae7d5ffe7c320ff6030f6e2 |
1.3258 |
0.3065238 |
33.5413409 |
| 0xcafd991099df144effe39de21286ca54e6eccd09 |
1.3257 |
0.3083198 |
33.7353271 |
| 0x4f36c619c9e9c159a81b2bdae463529a755fdb37 |
1.3257 |
0.3083198 |
33.7353271 |
| 0xbebb12128d82a89b5abb06b93c67e52a280bd70c |
1.3257 |
0.3093941 |
33.8528718 |
| 0xeb8b6d724210e26d4abf034e6b98eabb7ebb262c |
1.3257 |
0.2713241 |
29.6873816 |
| 0x12f1dbf4bbec01744f1da2f8cf51719c3cc27c82 |
1.3257 |
0.2713241 |
29.6873816 |
| 0x44abe66c01eb559a742f7667d3db08fe9570cf08 |
1.3256 |
0.307608 |
33.654902 |
| 0x539adc866f432e57f02966b647c534adf8856ad8 |
1.3181 |
0.2717323 |
29.5615888 |
| 0x726c9dd77ebe97d79c325bd8e2fc1c9a57eafdbe |
1.3074 |
0.3066404 |
33.0884275 |
| 0x26b8646bf1471ebc15c0a3bc07c52f5aac8a9224 |
1.3053 |
0.3081487 |
33.1977689 |
| 0x607b517548696509e50467d84ec84f62f59165d9 |
1.3031 |
0.3075812 |
33.0807859 |
| 0xa0d8a38b60e4dccf59b3f8040a820461521c2bb1 |
1.298 |
0.3093417 |
33.1399078 |
| 0x667b66278eacb153d49824f32b2339300b97afbc |
1.2926 |
0.2239885 |
23.8961516 |
| 0xf5208d0e44e1b84a4f310aeb3a9f41c6d001dafd |
1.2853 |
0.3087899 |
32.7571191 |
| 0x17541ee5135442a33820b060d996a4e445d4fadf |
1.2456 |
0.2732282 |
28.0893962 |
| 0xacd8330385277dc1d071a1605e551f46c89113f7 |
1.2406 |
0.2713241 |
27.7816732 |
| 0x3390594cd564c24349e0a59e5e9b7b4645db327f |
1.2384 |
0.3087867 |
31.561502 |
| 0x7ea18b7a65f942ea38657c6f544440cd070ef907 |
1.2355 |
0.3087898 |
31.4879173 |
| 0xda89ace3e8614106911aeb187ec2b923b605ed39 |
1.2355 |
0.308246 |
31.432463 |
| 0xad95985d68b30ebe5de1593c99b9c2e9a84d9097 |
1.2241 |
0.199172 |
20.1225663 |
| 0x25cea489d45e37b4c1810816294d37523e40b8a9 |
1.2241 |
0.2732274 |
27.6044736 |
| 0x7f102a66a4829868bfa883ee98bc4b3e37bb16ba |
1.2241 |
0.2732274 |
27.6044736 |
| 0x38761bf075cdc91bf826577067652301795c2471 |
1.2185 |
0.294314 |
29.5988392 |
| 0x8d418f795e1fa3d78532e7c11aed18706c6eed04 |
1.2144 |
0.273227 |
27.3856857 |
| 0x478386c5993639c980249ce3a50740e2c0845ff8 |
1.2089 |
0.3053755 |
30.4693179 |
| 0xe7bbb12e10be183e25244a4da4708003280cccfc |
1.1946 |
0.3076719 |
30.3353154 |
| 0x143ba89f42f0db0e2bb7f97dcfcc793049828d7c |
1.1946 |
0.2713241 |
26.7515636 |
| 0x806c8486aded0a44534cfd6e6603ce22720c42a4 |
1.1946 |
0.3082459 |
30.3919156 |
| 0x12afb841acdb523d034c9ce776b7a08af8823db7 |
1.1943 |
0.293894 |
28.9695912 |
| 0x748f782786426b02ccc52f880096ed774682205a |
1.1939 |
0.2008814 |
19.7945616 |
| 0x0dbe44eda689f9d3393678ab746062a4b3f36aaa |
1.1932 |
0.2556799 |
25.1795513 |
| 0x8cb87ad9943554f864d9e0f5bca1b8c78ee3df5f |
1.1872 |
0.3083736 |
30.2161587 |
| 0xcfb13a6e985a52e227fc3ecc854dd83d83ea8cba |
1.1872 |
0.2870061 |
28.1224587 |
| 0x27c9d372cb182f3c273668eefcbb7ff3fb39b334 |
1.1872 |
0.2732289 |
26.7724902 |
| 0x2c58f853b21becbf9abb59995c7ae33a6750bd0b |
1.1871 |
0.3089644 |
30.2715013 |
| 0x9b4abb199083a61f78ea34446b2aeccc375a8a4e |
1.1871 |
0.3093941 |
30.3136035 |
| 0x3c34ea3a77b3ce90ec4088c2c1e35c7686c0c976 |
1.1871 |
0.2713242 |
26.5836079 |
| 0x1ce5a568991afed9ba7aabec087e22579f9cbcf5 |
1.1871 |
0.2713242 |
26.5836079 |
| 0xfbd6207cac6dc88cb28c1d6c84583930db2ee061 |
1.18 |
0.3083736 |
30.0329039 |
| 0xdf2d9e58227ce5e37ed3e40bc49d4442c970a2d6 |
1.1785 |
0.3083198 |
29.9895025 |
| 0xf8308a8fed4382ca89d0bd5ac0cf859a98b046f0 |
1.1737 |
0.3087898 |
29.9128854 |
| 0x4222c1e579ca9d780887b96e5c2d0afc64249acf |
1.1722 |
0.309265 |
29.9206228 |
| 0x8e7fef28b08e6845fbeabd972a3bd963939ab54a |
1.1659 |
0.3076719 |
29.6065191 |
| 0xf0dc98562b74bd703558dfee50ea0e624701a4f5 |
1.1629 |
0.3087898 |
29.6376377 |
| 0x789cf302793b3b1c2602fb821a4d01ed9c9019c8 |
1.1629 |
0.2713241 |
26.0416798 |
| 0x2eb2478559a8c62a32323b14b4f9318223729b66 |
1.1595 |
0.3088065 |
29.5525746 |
| 0x46136533e43ed9032c89047a1fae76aa52543dcd |
1.1349 |
0.2713242 |
25.4146567 |
| 0xc9e791996fbc748dc6f5763488ddaded4ff925d5 |
1.1349 |
0.2713242 |
25.4146567 |
| 0x8c076d1f3ce0ca1c33fb96a625d8e9b1079cb6aa |
1.1348 |
0.2967641 |
27.7951402 |
| 0xd45f0805d99b8a61bb0320ac2d501dacf4517249 |
1.1348 |
0.2967641 |
27.7951402 |
| 0xebed9fa5c816cfad2fd70329e4cccc1f3322a072 |
1.1348 |
0.3002087 |
28.1177601 |
| 0x64dac40243cc1171e73533e4b75aeca296eae0a3 |
1.1298 |
0.219371 |
20.4559176 |
| 0xaddcacedef8a276f85851f2b654efb786f436a73 |
1.1278 |
0.2713242 |
25.2556609 |
| 0x5777acd69160215205590cc7e969664492cba55b |
1.1278 |
0.2713242 |
25.2556609 |
| 0xa00d08777972b1854514820cb93394d59c6bc3e7 |
1.1206 |
0.2732266 |
25.2703823 |
| 0x71af439d36551c2b42e1d34089ef26c7f572b271 |
1.118 |
0.2713242 |
25.0362027 |
| 0xfc4842d215753b38c66f0f903dc71f4c40d11ec7 |
1.1105 |
0.2696335 |
24.7132923 |
| 0x760ed6b61dbda0bcb56d81ce6e29e7bb8e21d3c8 |
1.1095 |
0.2988234 |
27.3640345 |
| 0x5f38c6bb41423831ed47e3ba7f9794a35ec2afb9 |
1.1063 |
0.2925915 |
26.7160911 |
| 0x85e9d8fc127e0d2e181e7385ebcb8c423a142a2e |
1.1024 |
0.3093941 |
28.1507173 |
| 0x939b88eb2578f81847fe4a806662649c7036af5f |
1.0974 |
0.308246 |
27.9190497 |
| 0x3c89cd398accfcf0e046d325c4805a98723f8630 |
1.0946 |
0.2550084 |
23.0381823 |
| 0xd85406790951ddfa23db571183063251048ee50e |
1.0899 |
0.2713242 |
24.4069387 |
| 0x6c9972422bd163b414ed422974ccc2b79b6a44f0 |
1.0899 |
0.2967646 |
26.6954326 |
| 0x03a40487a5015b4798e24695848b851f82df45cc |
1.0899 |
0.3093941 |
27.8315192 |
| 0x501b8ec4dfe26551dff42da66add6a2ff9177b07 |
1.0899 |
0.3093941 |
27.8315192 |
| 0x901cae80278238970780b89bec6c28953a459884 |
1.0883 |
0.3087749 |
27.7350416 |
| 0x45378505420b9b61ff06de2c71e225a5714f8ed2 |
1.0836 |
0.2736161 |
24.4708358 |
| 0xdb4f9986fb80a66aa24423fd325452b1c89715d3 |
1.0794 |
0.3088201 |
27.5122509 |
| 0x16b6493eacedaead7c6e5899b4b7c3508aa2cc91 |
1.0752 |
0.308246 |
27.3542574 |
| 0x0eb827290bfae1594146425431f725801fe37700 |
1.0752 |
0.307672 |
27.3033166 |
| 0xb5feb4e0976409249adacface0ffb17d262f21bf |
1.0711 |
0.2731723 |
24.1493235 |
| 0x4f2bbeb77f16cebca926fe5728d99ca01c4e9439 |
1.0665 |
0.3037808 |
26.7398777 |
| 0x31d9535f786ba1357f32aead0725465362571575 |
1.0619 |
0.2967646 |
26.0096164 |
| 0x0fa3d37a21c1a24867b5744473756f60a5f6730e |
1.0617 |
0.2714353 |
23.785176 |
| 0x8cefcce090a082130228302cb8297412098918ae |
1.0606 |
0.2732266 |
23.9173336 |
| 0x74449ab85bcb2707feec8fc51ec6b9b355d6ed0c |
1.0549 |
0.2793848 |
24.3249655 |
| 0x226e7dd7b3524bfbdf21a0079d51dfb350daecdb |
1.0513 |
0.3087423 |
26.78928 |
| 0xcb06a1988b64e2c4efe25594d7429f94b0850e6f |
1.0497 |
0.3087898 |
26.7526233 |
| 0x58c70c6d8d8a07c606ed85fad768e510b727143f |
1.0473 |
0.2717323 |
23.488242 |
| 0xc28e2583fcee2f7fd31ed9cfc892e49cee28e7fd |
1.0453 |
0.2789396 |
24.0651925 |
| 0x86fb349d84ac1f939be4fcaaa1cee027fbde52c7 |
1.0432 |
0.2713241 |
23.3611501 |
| 0x0398fc764a59826b21cf4f9e58fdc9bf017b3b3f |
1.0387 |
0.3048014 |
26.130353 |
| 0x4331ca43755629fc0d22a11e24abc28b36d7c218 |
1.0371 |
0.2967041 |
25.3969986 |
| 0x3acab0c6895ade28a29fe052cd62638f15aa634c |
1.0288 |
0.285827 |
24.2701464 |
| 0x38f693fea5a0a9762ec1e93ea2921ed7f3c86145 |
1.0287 |
0.2732263 |
23.1979441 |
| 0x80306a5e94e6c6a36e4a2f0def6c3666ddaf032c |
1.0272 |
0.2713241 |
23.0028502 |
| 0xa03ff9426c44e8bea91c82f43d6c0450761bb0a8 |
1.0254 |
0.3087898 |
26.1333152 |
| 0x3a77feff0b475ab67a451565b82a04d9f000a2e5 |
1.0217 |
0.3081557 |
25.9855424 |
| 0xe88902acf0e71101af3e990e1cc7a6625620afb6 |
1.0193 |
0.3093941 |
26.0286884 |
| 0x6fbf62db89091d1ba0a48918f792f68e141e5ee9 |
1.0154 |
0.2974287 |
24.9263283 |
| 0x0502edf91636645fb09f71d3cd421b05f75bc016 |
1.014 |
0.3089107 |
25.8528901 |
| 0x080cf7c73a6be337a2a2758a7095ff435e3df70d |
1.012 |
0.1991724 |
16.6359657 |
| 0xb01c9fd8dc4468117a33bfa1ad840e2938a9ae94 |
1.0107 |
0.3087898 |
25.7586724 |
| 0x978fd119e1a3013e7c0dbed66903faf913038bc9 |
1.0106 |
0.2799134 |
23.3475458 |
| 0x5013aedb6fd47f6da15b673ae53b102e8b1edb3a |
1.0099 |
0.3021427 |
25.1842308 |
| 0x7fe7e2d7f22133c78ad90bc36115c922be1a8706 |
1.0089 |
0.2717323 |
22.6270296 |
| 0x1a3a27b33c4c1efcb27ad76d6d501f511f59682a |
1.0009 |
0.2043341 |
16.8798968 |
| 0x8aa27e90e139d5ab5704df69429341cbcb2d2464 |
1 |
0.3013369 |
24.8708485 |
| 0x0eabffd8ce94ab2387fc44ba32642af0c58af433 |
1 |
0.297577 |
24.5605209 |
| 0xd5e9c8c55404afdc02065a8bc2aa612106f4247d |
1 |
0.2894527 |
23.8899815 |
| 0x0c8b9e3cb42ffbd1af7652b2824826cec8b75834 |
1 |
0.2924741 |
24.139355 |
| 0xa82082380585489b0456e15343c23809bc334709 |
1 |
0.3093941 |
25.5358466 |
| 0x138a15516d3e7e88ab20cd68305356c3c437d294 |
0.9997 |
0.2732282 |
22.5441275 |
| 0xcb4e7935859e485591e3aa6f7643d8cdcc901dfa |
0.9995 |
0.2696335 |
22.2430758 |
| 0xc8ae4de4ca42f277a6113ac0bd4bcec461d06791 |
0.9954 |
0.3083768 |
25.3348061 |
| 0x43fc29abad7ff4925a8eb306fb1bd22bd46b52a3 |
0.993 |
0.3069769 |
25.1589918 |
| 0x831c45ebc263e5a2bc28c254060de491ccfebe34 |
0.9903 |
0.3088201 |
25.2412268 |
| 0x252097d2491d7dac679a1826886426cd73edaf35 |
0.9903 |
0.308246 |
25.1943047 |
| 0xd9e10135bee11a553a4d947efabcb56892b1ee1c |
0.9888 |
0.3014002 |
24.5974521 |
| 0x14e9fa47944d0eb2ab041d37d821fd3548f0bf5c |
0.9855 |
0.3081855 |
25.0672734 |
| 0xed80a8ef1783eb1cac29777b144ba927be67ef6c |
0.9855 |
0.2713241 |
22.0690298 |
| 0xbe3c90d34b757587c62852dcd57f7c8e1bc5547c |
0.9792 |
0.2273055 |
18.370437 |
| 0x1bae19af613bd5db94baf043d5817e16a53a4c33 |
0.9775 |
0.3084808 |
24.8876064 |
| 0x2db372ed27478c56c499a57089939f83cf4dae98 |
0.9775 |
0.2696335 |
21.7534834 |
| 0x2569a1ae43285804944010c805b9b70023b2a19f |
0.9755 |
0.3053119 |
24.5815497 |
| 0x130cc6c031a0c4d5d71037555c88503b20a33695 |
0.9755 |
0.2894935 |
23.3079653 |
| 0x17bf04ac18596926fc2fb389965fc882f791c65f |
0.9755 |
0.3088839 |
24.8691344 |
| 0x0006a126d498aea76f845bc81fe1abe80c2697ba |
0.9746 |
0.3093941 |
24.8872361 |
| 0xc5c7680871474c4e74f29f721a9df732542e9fd5 |
0.9726 |
0.2896907 |
23.2544996 |
| 0x932dea7c05a2a65655d3eb226c046b4a99b86890 |
0.9675 |
0.2713241 |
21.6659433 |
| 0xcf4323e5c1330e0aaac7bb50442634a9724c9f8e |
0.9607 |
0.3087423 |
24.4806065 |
| 0x546f796a73958dffece003f61bf16e4fbdf34dc6 |
0.9557 |
0.3087898 |
24.3569428 |
| 0xe08a5e0b822e4a59830d2b611ce7ac51090c071a |
0.9504 |
0.2273001 |
17.8297122 |
| 0xcd48e7c6943805edc7c8a9b2bdf67e7695733313 |
0.9497 |
0.2990306 |
23.4390695 |
| 0x596af307b7b1f8741f9cc7d74a20be2960de4750 |
0.9487 |
0.2717323 |
21.2768983 |
| 0x22609be83d543c4865760afeeb6ee1b5fb4f9036 |
0.9408 |
0.2713241 |
21.068031 |
| 0xea9aba09189cbcb9545824ac6650f8f075b693f6 |
0.9408 |
0.3081856 |
23.9302802 |
| 0x0180148fc2e53362b66d48ac33907c0cedbbe9d1 |
0.9301 |
0.306977 |
23.5653379 |
| 0xdaa255e8bbd998675a0fdb3ffc13a9f9fe38158e |
0.922 |
0.3014015 |
22.9358346 |
| 0xa1013f68dea21d0505a0b7084e57cc5eda6d2760 |
0.9181 |
0.1991719 |
15.0923237 |
| 0x28f5d02ec235f9418fe2a6f4e90d12361a00b9e7 |
0.9181 |
0.3088201 |
23.4009605 |
| 0x97538e1a3821f3327fe2a2ff4993f3d154f28b01 |
0.9181 |
0.3089107 |
23.4078264 |
| 0xef191aeb45a0d6f393d4a592f94152836d5758f8 |
0.908 |
0.3065087 |
22.9703144 |
| 0xee40b443109078e209848ba3229d215a037f6a37 |
0.9027 |
0.3041283 |
22.6588792 |
| 0xc6d7a78707878f94e8de99cf4d74456b69d38fd4 |
0.897 |
0.3081123 |
22.8107568 |
| 0x4ff9f2a2d413ed73a28650c58bb3d0fd3d2f0a9f |
0.8959 |
0.3078633 |
22.7643678 |
| 0x9fefead7ff47b609161eb6b4a6b95e9549216732 |
0.8959 |
0.3066749 |
22.6764957 |
| 0x7b980f5a98804964a653affd86e6d4b3bf266396 |
0.8959 |
0.2990608 |
22.1134941 |
| 0x4b1f8fb27699ca736cb46c1bf2794fe92fb7daa5 |
0.8959 |
0.308246 |
22.7926679 |
| 0x7d1dbe2ff94be8da44200ab9cad2d78617fbc120 |
0.8903 |
0.3069769 |
22.5569433 |
| 0xa923e6ed4c775d4180db2f1532a5d5bdbb091c1d |
0.8903 |
0.273227 |
20.0769721 |
| 0x8477997b959b4f9c49146f1364ce789fd0de5eab |
0.8819 |
0.2875259 |
20.9283308 |
| 0xff64422f65e6a5fe26309366df66a5467378cd04 |
0.8787 |
0.2979623 |
21.6092761 |
| 0x1235957b8419496e37765c3984e863a22bc5a494 |
0.878 |
0.3070958 |
22.2539221 |
| 0x3dbab2b64a6caaa8a722af8e9263665c0af89c37 |
0.8722 |
0.3087898 |
22.2288651 |
| 0xcdd611fbc544e66b9a42f55d60155628aedcffa9 |
0.8722 |
0.3087898 |
22.2288651 |
| 0x50f2677340c2a6c6557c475e6282a2b475d1b85a |
0.8722 |
0.2713241 |
19.53182 |
| 0xa191fd04ebf22bb9317094557cad0cf68d0767cf |
0.8716 |
0.2894935 |
20.8254405 |
| 0x095ff8acd86e3c3f52bc4705540a0803ffbaeb37 |
0.8715 |
0.2951049 |
21.2266725 |
| 0x360a0860a57cc9b234ae30d92afc49d0fe18276f |
0.8715 |
0.2755541 |
19.820407 |
| 0xfbc3eb42da712a7e1d0b9808359e98dbf282b6a6 |
0.8458 |
0.3083198 |
21.5232235 |
| 0x84037f0d36c6bd21ffd9b6c11f671ba100bc9bcf |
0.8241 |
0.3083586 |
20.9736569 |
| 0xebca9bf3394d4e14f936f74d71da3f39f8f3c68f |
0.7955 |
0.3075811 |
20.1947338 |
| 0x7a9b80c93c7a02287246277291e0ad587fa8719e |
0.7911 |
0.3088838 |
20.1680904 |
| 0xd94961c033529e58a8696dbb351f55225b05b6c5 |
0.7802 |
0.2979126 |
19.183725 |
| 0x5db6da215709e39945345f2024fa868a68563393 |
0.7716 |
0.3081855 |
19.626491 |
| 0x82f096c7e815886f9d837fb882d2cfccfda88944 |
0.768 |
0.1933714 |
12.2572064 |
| 0x9ba2fb823d8ace249f166b0e6a3d2515bb0257f9 |
0.7568 |
0.3093942 |
19.3255287 |
| 0xa91e1b5b54d845acb57b5ae877bb5218fdfc8001 |
0.7557 |
0.3081855 |
19.2220575 |
| 0x7516681df995ebd6fcf1555cfa6470cb4a816b56 |
0.7554 |
0.3081856 |
19.2144286 |
| 0xc3fd78a0e8859048cdedcbfcc972b3ba17b0b9d3 |
0.7544 |
0.3082459 |
19.1927519 |
| 0xa5f869e121ff8b100f27ae3c84d2632fb6299f9d |
0.7479 |
0.3093942 |
19.0982597 |
| 0x5c70940b0f95609e9f82908f778136b46a7f3e22 |
0.747 |
0.3093941 |
19.0752774 |
| 0x93777e65880378fbb336f595ab902e5782172c38 |
0.7469 |
0.2966977 |
18.2900437 |
| 0x4ee7290a442be8ba264538f4cd12d4cd8125c1b1 |
0.7469 |
0.2822698 |
17.4006334 |
| 0xa4dce84f3c7798892cc71dc3b4930dbc0ffe9b9d |
0.7447 |
0.2732259 |
16.7935059 |
| 0xc3cf2d1505c350f56580a1710f6e5376ed443882 |
0.744 |
0.2153942 |
13.2265056 |
| 0x866d01b6c410aae251a0666515ec7ea8c4386edb |
0.742 |
0.1991725 |
12.1975163 |
| 0xe68ff9ab9bfcb3711aafbb2707a469c53fd859a7 |
0.7403 |
0.3081556 |
18.828515 |
| 0x56b8a0f575424a4e10da4b8d9dd7d70b8848db3d |
0.7196 |
0.308246 |
18.3074049 |
| 0x3cf7d788960a44c3da4e25fbea530d78e61e3853 |
0.7196 |
0.2732287 |
16.2276507 |
| 0x3815f232b5ff0a5ce2e887fc743f91fe126377b3 |
0.7196 |
0.2732287 |
16.2276507 |
| 0x7fb8093bd075f3e4174f2eccf7883ed43de8cd8d |
0.7163 |
0.2273002 |
13.4379456 |
| 0x463f19f579c141eae280558605afe8ed4b81821c |
0.7093 |
0.2732295 |
15.9954245 |
| 0xdeaaa6111c55164c2c38c69f69f0f7c56d422143 |
0.7093 |
0.2732295 |
15.9954245 |
| 0x5ebebf0ab55445b8de48393fbced747be0c6013f |
0.7093 |
0.3088201 |
18.0789708 |
| 0x0671aec56bc2e358448162677bd110d673cd2937 |
0.7093 |
0.2870065 |
16.8019582 |
| 0xd44cd72ebd12b73fa5d59d603ffd9e8cdbc71b3a |
0.7093 |
0.3088201 |
18.0789708 |
| 0x2ae90f28f678ad4c43fad0b9dbcd7b7971ac948b |
0.7092 |
0.2713242 |
15.8816399 |
| 0xa3a50300902320acfe4bbfd58d475d58b2419ec2 |
0.7092 |
0.3087899 |
18.0746521 |
| 0x9f8a4ed477b1b5fcfc5c423066c5c63411abc552 |
0.7062 |
0.3093941 |
18.0334149 |
| 0x4e63b3ee1eab9c7c57242505b13c99e0e1980c11 |
0.6977 |
0.2713242 |
15.6241141 |
| 0x46642e15d77bbe0bdfcfbf348c38b06153d16049 |
0.6956 |
0.2956169 |
16.971762 |
| 0xbec6c2e2c848ba012c39afa533aa22c35f11a85a |
0.6956 |
0.30882 |
17.7297777 |
| 0x8a1d7bc021b56d0dd8a297aeeed121b67a18f0d9 |
0.6956 |
0.309394 |
17.7627349 |
| 0xbb8b354b59ce349efc834ce761b3a7f2044c25ef |
0.6956 |
0.2732287 |
15.6864312 |
| 0x32a8f8e64682d4dc66ea16c6cc84e3abba867808 |
0.6956 |
0.2732287 |
15.6864312 |
| 0x882c6d8eaf516654e0694e75bc7041bd086ae71e |
0.6956 |
0.3084273 |
17.7072232 |
| 0xd8937ebfa74d5adeb50af3f6f3bf91b65a213ee7 |
0.6858 |
0.2858271 |
16.1785261 |
| 0xf2c6c25d1b94c20e23c7408c317fbe975c642c69 |
0.6858 |
0.2870057 |
16.2452417 |
| 0x30dec1e809736b2c9ac30200a84cc650d2232acb |
0.6858 |
0.2513828 |
14.2288929 |
| 0x779c9a1c80ccb9b2a00071b7afd2b9fdb49937b2 |
0.6858 |
0.2732282 |
15.4654025 |
| 0xb26145160a80616dc909885aeda90af97eea349e |
0.6858 |
0.2732282 |
15.4654025 |
| 0xd1d7140ab46e3889267409758f244c57eadcd4e8 |
0.6858 |
0.2915981 |
16.5051902 |
| 0x8ecd1f436b3e9c242b5ae32140be4350e66b08e0 |
0.6858 |
0.2713241 |
15.3576284 |
| 0x5967eee77e4db6d8638dde8b55682bce8aa6f935 |
0.6852 |
0.309394 |
17.4971621 |
| 0xb8d95c72abac437f4a3b90e53bcce5a5133eff54 |
0.6709 |
0.3087867 |
17.0983624 |
| 0xfb50a94d5ca985e349ff78f3bc401cce9c142d35 |
0.6695 |
0.2004052 |
11.0738274 |
| 0x429bdfe47125fdc2eb94035f2e2acaea8053ce39 |
0.6663 |
0.3081447 |
16.945824 |
| 0xbc7c96d0f927d6e883a069cede9d6a891cc7e301 |
0.6629 |
0.3089107 |
16.901264 |
| 0xc3c487e055f1e097831a04535c9f0f52140c3bea |
0.6629 |
0.3085346 |
16.8806916 |
| 0xab4f01e48d3304516ba6b925132d8695ea4fa657 |
0.6629 |
0.3083198 |
16.8689356 |
| 0x43d864846502675c7ad44bab1a132bc197ea0ddb |
0.6629 |
0.3075812 |
16.8285283 |
| 0xb6e3633baca360f52d51c88b2a1b00200275e54b |
0.6628 |
0.3083734 |
16.869325 |
| 0x1e3add23df3545bd2c07fc96dbf88f752b67863e |
0.6628 |
0.2767339 |
15.1385021 |
| 0x240b6283e08973a01b3823c59095365b19c25c60 |
0.6628 |
0.2732253 |
14.9465747 |
| 0x464d61041513059747268c5aa17f36b4cc960428 |
0.6628 |
0.3013567 |
16.4854733 |
| 0x4739b3c1cd96000ba2bbb0bd38d62deb2e50cd1f |
0.6628 |
0.2732253 |
14.9465747 |
| 0x8f90628fbf475ded16a83071edcd1d21b764017d |
0.6628 |
0.3082459 |
16.8623473 |
| 0x1f64d08198991c3c0d794d2fc52c458ef807787c |
0.6593 |
0.1991787 |
10.8383709 |
| 0x075cc3b601b618bd349f435efc08c502ca2753d0 |
0.6593 |
0.3088838 |
16.8080166 |
| 0x36c023243a4f8483eba8c4a387646f7c60b0856d |
0.6515 |
0.2906612 |
15.6293107 |
| 0x101ca29e628354bcd49f23ddcb6e418c1e74d9a4 |
0.6487 |
0.3087867 |
16.5325806 |
| 0x745d9f9c9f01c7d8afb63e81d16c60f2fb74a1e0 |
0.6297 |
0.2884456 |
14.9911794 |
| 0xcfdda69723fc8e9b86c0430e45b2de6ca1b2f51f |
0.6272 |
0.308246 |
15.9566515 |
| 0x66391500a1889ed8be066c75f248b4b3b7d08168 |
0.6228 |
0.3087898 |
15.8726641 |
| 0x3a49c4c67b2efc6439cb80ff2f613a823d799c65 |
0.6228 |
0.2737993 |
14.0740531 |
| 0xc4e3a14573e79ca3b626ba1936b4ae636db91c86 |
0.6177 |
0.3091072 |
15.7588604 |
| 0x6ca92470dd3e4d60de70bd26793fd9dda7fb5761 |
0.6177 |
0.2732286 |
13.9297054 |
| 0x1cc392f0ebbacf82f8a53945a5a16896f1fdec5e |
0.6177 |
0.309394 |
15.7734924 |
| 0xe8d0492bdca82bb0b4104e04affb709536c85e87 |
0.6153 |
0.307672 |
15.6247525 |
| 0xeba24c5fbb3615e375c269a661abd6acf063d876 |
0.6121 |
0.30882 |
15.6014894 |
| 0x79927c91f77edb84677a588b96ba5cc16e2803a9 |
0.6117 |
0.2795012 |
14.1110833 |
| 0x81f7a5244a87eac618cdf55751289cc47cd5c634 |
0.5973 |
0.3081855 |
15.1929797 |
| 0xb55b77157f3b341b979c1b59b2173484461929c9 |
0.5973 |
0.2732299 |
13.4697314 |
| 0x61a1720dede07b7474578ee9178c721308e5b81a |
0.5936 |
0.3081855 |
15.0988673 |
| 0x1019236722517506732d92dac0f7b9b4ed993d8d |
0.5935 |
0.3068158 |
15.0292279 |
| 0x8469ca0696419f15ed5a9a0ac7c90bf9c3091ea4 |
0.5935 |
0.2729452 |
13.3700905 |
| 0xef077bcb6a3f54c927f829d806a3a36860826ea3 |
0.581 |
0.2698434 |
12.9397604 |
| 0x6a7bbac98651ddfea68d2eca6e4200dc4dac05d6 |
0.5674 |
0.2732296 |
12.7954446 |
| 0x35d0445a9183a6dd55bb4e2ef69e37bfcddd566b |
0.5639 |
0.3083197 |
14.3496647 |
| 0x0855895639c19c3dd7b17ab17d5c92da19062261 |
0.5613 |
0.3083736 |
14.2859943 |
| 0x13aeb98cd578b0734717bea0c0d13ea124f88450 |
0.5552 |
0.3093941 |
14.177502 |
| 0x93a693d479fcd11eeb160e7573317b6054726421 |
0.5487 |
0.271324 |
12.287444 |
| 0xb4cfe63fe89ec621959462ff811fdcc3eeb40e29 |
0.5469 |
0.3085632 |
13.9280487 |
| 0xdc11a7d82aee95cefb66c6c51bc8e8c46cd9e303 |
0.5391 |
0.3045598 |
13.5512737 |
| 0x3791b96ae2e3140e36274be6a3b298be09a818cf |
0.5303 |
0.2732265 |
11.9586668 |
| 0x66f9f7835e1dba9dab8f43161df1732df7f13efb |
0.5303 |
0.2732265 |
11.9586668 |
| 0xee78c5d6220628b63bc5c0a169122d5d37f523d3 |
0.5303 |
0.2713242 |
11.8754008 |
| 0x91e6e15765007fb8538eb5ccc90c2c85d79c5591 |
0.5088 |
0.3087899 |
12.9672625 |
| 0x3a88cf9c05cb64cad550e9f90c360ba748e06b02 |
0.5077 |
0.2930784 |
12.2808717 |
| 0x40dc654af5ce40c122ffdc679fa8e8ca8b91556a |
0.506 |
0.3093941 |
12.9211384 |
| 0x66dc472b5befadc076688618fc22159be31fc946 |
0.5036 |
0.3087897 |
12.8347347 |
| 0xf39195f0a7b804a55fe861a17e1d021656c0196b |
0.5 |
0.271324 |
11.1968686 |
| 0xf8b62952c3e36a862a1104adfcf036f8e916b8b1 |
0.4896 |
0.3070978 |
12.4095628 |
| 0x4fe417394bd9739a11841ff81803838b6929b798 |
0.4878 |
0.3088838 |
12.4358424 |
| 0xc2e6b265cb965ded721566f0f9eb5ab1a6162a21 |
0.4801 |
0.1991712 |
7.8921726 |
| 0x216f91ce3c1cb358e583441d6179c6c19c834a2e |
0.4651 |
0.3087899 |
11.8535261 |
| 0x4f548006cbfba0b08304001b97025a148ee32031 |
0.4538 |
0.3081792 |
11.5426655 |
| 0xa0e24f71b048db3f8a8bfdb080dd79315dc82f07 |
0.448 |
0.308246 |
11.3976059 |
| 0xb632ef220a6ade029d79f794f466ca2ef315ab24 |
0.443 |
0.2373275 |
8.6774126 |
| 0x6eed6d0b620c01627893af99521b7092311cb9ac |
0.4416 |
0.3088571 |
11.2570534 |
| 0x40b4f2f7c39b7e23d80e4b32db676557b9756371 |
0.4358 |
0.279458 |
10.0517615 |
| 0x09f9f637f29e922f94cc63dae8fd830a2a804f5a |
0.4301 |
0.2705192 |
9.6029722 |
| 0x4a3d79b061fed2421917b06b421c44ad9489410c |
0.4256 |
0.2732293 |
9.5977022 |
| 0x4a0cd366ddb8aba3055089e5a272af1a85fc7f79 |
0.4256 |
0.2732293 |
9.5977022 |
| 0x90d1d211c8d3a94698b8d1b4fa4019add4d81543 |
0.4184 |
0.2732259 |
9.4352112 |
| 0x8a29e6e1fd4993e3d6becbb20eebbc03e11d073d |
0.4115 |
0.2732299 |
9.2797522 |
| 0x0cb047c76552f2d9e39ee227be8d6d4c57503c46 |
0.4037 |
0.2767372 |
9.2207101 |
| 0x225e6d967f55f8222800797baf9e83d976e2349d |
0.3901 |
0.2273009 |
7.3183853 |
| 0x487a86796f6897f5f60db95d44afbbff73365ccc |
0.3881 |
0.2950711 |
9.4516691 |
| 0xc01628226276146ebe20c0fd043f73ba590a2479 |
0.3867 |
0.2272943 |
7.2543861 |
| 0x34a4c76a57501b298d831a710e70adb7ec240075 |
0.386 |
0.2713241 |
8.643983 |
| 0x75b521f3ec9bd577ab1d74d58bdbc0a1a7b0d671 |
0.3784 |
0.2702851 |
8.4413465 |
| 0xe461328bd38c516f35d5a1744389ccc8a28eab4c |
0.3784 |
0.2702851 |
8.4413465 |
| 0xf3b25c2a249272814ebcd6031742a4394a9644e6 |
0.374 |
0.2702853 |
8.3431931 |
| 0xb98021ef7ae53655dc10603275031e6e13564569 |
0.3728 |
0.2846513 |
8.7584475 |
| 0x8fc0ada7f4a93ed9e87a087bbacaed63c5407c6c |
0.3689 |
0.2702852 |
8.2294213 |
| 0x5243c3faf2fc7909082c857634ad2e61143add49 |
0.3595 |
0.3087424 |
9.1607966 |
| 0x675d882d6cdcdd8b2eaea95f21fbfc6916af89f8 |
0.3578 |
0.2960302 |
8.7420758 |
| 0x897434238a4c076fb10e56f8fccce23bb75f5565 |
0.3561 |
0.2732272 |
8.0303407 |
| 0x2c7fba545fec4060c689046c28ff0ddb11a91776 |
0.3546 |
0.2732245 |
7.9964355 |
| 0x157c6444ab68a6f1e51a4757a735c19d96f0ee3d |
0.354 |
0.3093941 |
9.0396897 |
| 0x6a9f76ca688e39cedd71328e100dba1e867ae5b6 |
0.3464 |
0.3081856 |
8.8110641 |
| 0x0f0a6119674c021f490de259c463cf351ff6c417 |
0.3446 |
0.3041796 |
8.6513437 |
| 0xad987861f38c384272dafb6d952fbf97cdac5e18 |
0.3441 |
0.3088178 |
8.7705131 |
| 0x1a8bbd640a2424c07c2d4ccef881a496251ce971 |
0.3429 |
0.2272908 |
6.4326106 |
| 0x34e078afb3e89df97c1f7cee7b91b14a9236079d |
0.3429 |
0.2732228 |
7.7325448 |
| 0x7242b3789e6f53c881bcca97f8d218387207da45 |
0.3342 |
0.2207475 |
6.0889237 |
| 0x1338ccaa10126a32947180f5771b4590963b81df |
0.3315 |
0.302336 |
8.2720247 |
| 0x3bb5ce666d4ece0bd5be0c7201b657ce57c9bb46 |
0.3315 |
0.3082462 |
8.4337209 |
| 0x90978ef87b3ef9f3cd11a5e82c8ef57b04d77e76 |
0.3315 |
0.2732305 |
7.4756829 |
| 0x3c5af5ffe13e7be9bfef1862e6f80769c69a9206 |
0.3296 |
0.275017 |
7.4814349 |
| 0x809bb406235e118a77b246dde0ba1e4fdb73a68f |
0.3264 |
0.2339188 |
6.3016373 |
| 0x0a76834367d68b35457bbcfbaf5ca390ab2b8d57 |
0.3258 |
0.3087897 |
8.3033284 |
| 0x507b94ab08fc400379706e0157bf342d95ee2f7f |
0.3238 |
0.2732288 |
7.3019945 |
| 0x15a29b54e3f66999daf38cff4d9f29c8d3248c33 |
0.3136 |
0.3065571 |
7.93461 |
| 0xa93883c125a4f26001720457253448116c60ff67 |
0.312 |
0.2735571 |
7.0443474 |
| 0xc17e1e59a83a394fdfb365b8159e712d7fe6ee0a |
0.3096 |
0.2822733 |
7.212884 |
| 0x610dce6c9cb8e035ca7ebb3f7e3df1674c1572ad |
0.3096 |
0.2274548 |
5.8121151 |
| 0xa44080bbdc8be2dcb43873db457d02a3207f896d |
0.3088 |
0.2732228 |
6.9635743 |
| 0xa6afebe6b3545de9148ac7078fb4d548f342fc78 |
0.306 |
0.3082461 |
7.7849731 |
| 0x0a213502fc59cd3512590534d3f99e19995f1b2a |
0.306 |
0.3076719 |
7.7704719 |
| 0x2074d5855c9b555091d9b6ffeeeaff7e89158bff |
0.306 |
0.2738016 |
6.9150562 |
| 0x166a31ea1c1dda5586e27cf1ef0f677788866bd0 |
0.306 |
0.2719284 |
6.8677446 |
| 0xb2eb4f13a0b4cb237cdb809353d17ea90ba8a418 |
0.306 |
0.3093941 |
7.8139691 |
| 0xa95f856f2835ae2a61b2360b3de4f0ff2b39d91b |
0.3036 |
0.2960998 |
7.4195583 |
| 0x4d691b5a9bc1d4c5893d5c5a1e3907e9fc66509b |
0.2986 |
0.2732237 |
6.7335889 |
| 0xaec21c8d0e2ec54861fec7998a25ea9e595f8bb1 |
0.2986 |
0.3093942 |
7.6250038 |
| 0xbb757f8777dd30776d610dc68e10a6d76aadfea3 |
0.2982 |
0.3075198 |
7.568659 |
| 0x0a9d7689d5e2b9e0b007914a2654c40b6f56db05 |
0.2968 |
0.3093942 |
7.5790393 |
| 0x41801a2163c53144388386218c65a16e4c818674 |
0.2968 |
0.3081856 |
7.5494337 |
| 0xaca8930e85b9beaed1371d4e7e1b586147d87e80 |
0.2968 |
0.3083066 |
7.5523958 |
| 0xd603e8b1b99b4b4379280cac86066051602782b3 |
0.2967 |
0.3058217 |
7.4890031 |
| 0x97e47879a4f2aa46ee3043612db08dca498bde4d |
0.2967 |
0.2967631 |
7.2671732 |
| 0x944de1cc15d4916f68bbb018c4ae274141904a56 |
0.2967 |
0.2732231 |
6.690727 |
| 0x8d8c356b972e54e6ff1422da859cd4b0f9880b60 |
0.2905 |
0.2755542 |
6.6068034 |
| 0x55ed592cab970d34d7fb3f6cc0427268264fe7b7 |
0.2905 |
0.3032702 |
7.2713323 |
| 0xe2acd09ef81fce015f0bf0ec08ac9edd839075b8 |
0.2905 |
0.3093941 |
7.4181634 |
| 0x86c173479cf6c2a5caa6a75cea15a44d0218d21c |
0.2837 |
0.2273067 |
5.3224237 |
| 0x3a2f6a462fd2e7c19ff272348bee4a13f3e7c388 |
0.2826 |
0.3093942 |
7.2164303 |
| 0xaf7e030dcebfa02bdb7ce8ec51755baea960c352 |
0.2582 |
0.275017 |
5.8607609 |
| 0x1de9338650f8c2fa0e24aded1aebfd27c72b788f |
0.2482 |
0.2272985 |
4.656251 |
| 0x7b69785643c0428e74659c9824d85ce0299a66d4 |
0.2404 |
0.3093939 |
6.1388175 |
| 0x1b9da462d07512fa37021973d853b59debb761dd |
0.234 |
0.3041607 |
5.8743108 |
| 0x2d6f477b0dab87dfddac0d385b3b269e0672271c |
0.227 |
0.2713242 |
5.0833795 |
| 0xe540302d3b59c5fefeb9967eec7201eccd5327cb |
0.2234 |
0.3093939 |
5.7047081 |
| 0x1046394abffeec81be8c48136745a4a46917ccbc |
0.2159 |
0.2852895 |
5.0836636 |
| 0xcef37652b08fdca63ae5006e84015a697ab856c8 |
0.2127 |
0.2272877 |
3.9900814 |
| 0x37a3b587300f79a9af4c80a079e1e83df1119b50 |
0.2058 |
0.3093941 |
5.2552772 |
| 0xd4363403afd7caff80b40b834131dd2bcfe31464 |
0.2058 |
0.3088095 |
5.2453502 |
| 0x9235e63508e8d27e0cc858d059c752f8de4733c2 |
0.2002 |
0.306977 |
5.0723352 |
| 0x79240ea3dba4f6e58a77192c9c24dd57bc79304a |
0.1989 |
0.2713243 |
4.4541156 |
| 0x437b28a6ec8e76556d99fa571006ea5da594aa91 |
0.1988 |
0.3027591 |
4.9676574 |
| 0x5513c575fc4cb3fe01fbd407a3fe9108728de308 |
0.1955 |
0.308356 |
4.9755097 |
| 0xb413e15ebb6669a3dac9bb30fa6ff076aaaec439 |
0.1929 |
0.2864759 |
4.5609863 |
| 0x424fc98e3356da0e5a998a50c91859c1113e6b5b |
0.1912 |
0.3065246 |
4.8371692 |
| 0x032c80ee9661e748bf872fa23b134013c44d8cea |
0.1851 |
0.3087461 |
4.7167837 |
| 0xf33818edafc0803beaa2a8ae829be38a2bb06f23 |
0.1813 |
0.2273188 |
3.4015056 |
| 0x192e12cac6e84d4c29e2a503ef3e0c361c65f9b0 |
0.1688 |
0.308282 |
4.294957 |
| 0x3a059ca2b7cef069f021005e4713dfbeb91c5906 |
0.1577 |
0.3086709 |
4.0175867 |
| 0x7fdcd78669591bc6bf7a9e9925acd8ad55061fd8 |
0.1485 |
0.2088936 |
2.5602942 |
| 0x30515e60b426ce67adf106fa95c172b23566eb6d |
0.1439 |
0.278943 |
3.3129505 |
| 0xe77cb45299689fb5b65a357d61e1f95099a4b687 |
0.1397 |
0.2341367 |
2.6996274 |
| 0xb77c2676fc30dd05e7823123278a76b67b42f8d9 |
0.1382 |
0.307581 |
3.5083763 |
| 0x0ff9b6ab6ec58ceb6d5ae8a1690dd5a0959ad002 |
0.134 |
0.3040627 |
3.3628412 |
| 0x5259daf51a4311637216ece9c005e6f551114a4b |
0.1335 |
0.3073566 |
3.3865831 |
| 0x53daea9e1ba020c6c9b1c284b282b527215aaa7d |
0.1326 |
0.193371 |
2.1162833 |
| 0x76ae174540ab0c73e9ed81a902415cd259292d12 |
0.1315 |
0.2496487 |
2.7095225 |
| 0x787c8be38e968bd0b41eaabe0b69d1c32ea09262 |
0.13 |
0.3042915 |
3.264908 |
| 0x972a8b7d891b88220780421fe4d11f174354ceed |
0.12 |
0.3042917 |
3.013763 |
| 0x119383b0051e920d6161cee971247d625b8d69cb |
0.12 |
0.3042917 |
3.013763 |
| 0xb2dde7601a83cf17d14fa8ad15b27b60656579c0 |
0.1191 |
0.3081797 |
3.0293781 |
| 0x2f83c624b64a25399a4567cba4d46dd5f45c5421 |
0.1111 |
0.2716382 |
2.4908207 |
| 0x9ba6baa919bac9acd901df3bfde848fe006d3cae |
0.11 |
0.3078636 |
2.7950452 |
| 0xcaa13b991403ceb897ab25a0b4e49849073360c6 |
0.1086 |
0.2272781 |
2.0371605 |
| 0x7b203e83480ce8cea0590336400799c4b3c2a28d |
0.1083 |
0.3081791 |
2.7546731 |
| 0xb3993c9280a6125009b530dd79b1d2a6ebb618e6 |
0.1066 |
0.308742 |
2.7163853 |
| 0x93ce05ddfcacff4a4c1a1b4f212ea207ee418e66 |
0.106 |
0.3085887 |
2.6997518 |
| 0x14481d6ac7925b3b14372b0b7319d0af445cca6a |
0.1012 |
0.2713241 |
2.2662457 |
| 0xb1fbad53fd06082d884c90dbd66c68613453bf20 |
0.1 |
0.309394 |
2.5535847 |
| 0xc46c67bb7e84490d7ebdd0b8ecdaca68cf3823f4 |
0.1 |
0.308742 |
2.5482062 |
| 0x3edd888f0e05610a0a3c5ec02e687fea05424977 |
0.0877 |
0.3093945 |
2.2394937 |
| 0x19ca4ba7a3ef4eb9b0eefdff8db4813a415ac04b |
0.0832 |
0.3082428 |
2.1166791 |
| 0x451da770733cd8c66b3bef38130842df0c730c8a |
0.0787 |
0.227263 |
1.4761922 |
| 0x1522c627472ce025df05d9630fa51779683ba698 |
0.078 |
0.3088205 |
1.9880997 |
| 0x33d29ceab11333488667e1e79bacb6ed6f08d392 |
0.072 |
0.2081764 |
1.2370905 |
| 0x608797e5216b9793b41b363c19c55d24c5d2383a |
0.0709 |
0.3088195 |
1.8071304 |
| 0x1b31df177e13722c3e9f090f79e9af20e7e3b16f |
0.0709 |
0.3088505 |
1.8073091 |
| 0xc55d4b1c1f626493ab0ad9c792e075d281fed315 |
0.0686 |
0.3047988 |
1.7257444 |
| 0xd97b87d23e9e3f0ca5428508fe8561e2c9057fbd |
0.0663 |
0.1991463 |
1.0897423 |
| 0x4630cf0fa55f83e11e43286ff04fc6930e1eb095 |
0.0659 |
0.2282656 |
1.2415465 |
| 0x5ddf8b02510d54d19667932ac59cf03b617879a8 |
0.0659 |
0.3088847 |
1.6800385 |
| 0xb220563b0f237f79c1d12d887c3a9d9c17bc35b0 |
0.0652 |
0.2858267 |
1.5381166 |
| 0xf169c32c74442eabbf5991919c1a7636cbd02131 |
0.063 |
0.308319 |
1.6031724 |
| 0x58085ddc6050825495060735b8a41999150879e2 |
0.063 |
0.2750175 |
1.4300074 |
| 0xe3f96cb5ae6353ed964f12c3841f50c8453df33b |
0.0592 |
0.2696334 |
1.3174486 |
| 0x77aa24edca9cd282c9bf953fe388751be47b04d1 |
0.0507 |
0.2272426 |
0.9509007 |
| 0x9aa63df87fbfac27eab23b0f6c31839bda59cded |
0.0507 |
0.3087909 |
1.2921394 |
| 0x302186e737266c5f10d2bd5b0f98cad1800fb588 |
0.0404 |
0.2732079 |
0.9109913 |
| 0xc5024e68ff693592b2aba7bde36519a69d8fe027 |
0.0383 |
0.3087911 |
0.9761141 |
| 0x6a242fe418ac550d425c3aa0b20795fa28b1a122 |
0.0369 |
0.2702846 |
0.823164 |
| 0x065efb8cbd9669648f4d765b6d25304f66419c47 |
0.0354 |
0.3082429 |
0.9006014 |
| 0x2d5823e8e8b4dfbf599a97566ff2a121cc141d60 |
0.034 |
0.3042912 |
0.8538996 |
| 0x95e9bedbc090da23fd2975c38505b59c24143a9d |
0.0309 |
0.2751424 |
0.7017059 |
| 0x36edbe1eac1cef4cfc346b9c5b91f09a9534aae5 |
0.0306 |
0.2719281 |
0.6867738 |
| 0x3345092b19cf6159c7da1c65ed9542609bc3a001 |
0.0306 |
0.2719281 |
0.6867738 |
| 0x0516cf37b67235e07af38ad8e388d0e68089b0f2 |
0.03 |
0.3042933 |
0.7534415 |
| 0x79ccedbefbfe6c95570d85e65f8b0ac0d6bd017b |
0.03 |
0.3042933 |
0.7534415 |
| 0x504d1537edaa08adc950507c8ad7a35c6581a379 |
0.0299 |
0.3093946 |
0.7635218 |
| 0x5e7018bf8c7615436cb738099452cc0cd67145f1 |
0.0299 |
0.2719264 |
0.6710629 |
| 0x385cc6de9901bdd59c366b736e27221c679f7324 |
0.0299 |
0.2751438 |
0.6789982 |
| 0xfd1f64fb704c015008f3fda0d0d0c51dd9cacd73 |
0.0297 |
0.2719293 |
0.666575 |
| 0x0e2aeeaa52752e111ffa3609409bc6bb55a87ce7 |
0.0291 |
0.2784983 |
0.6688923 |
| 0x30d0aa20bfe31156a9964aa997b3468ff57fc29c |
0.0291 |
0.3093952 |
0.7430931 |
| 0x14b1fd38a4c16be4031998f0f79cb95d4cd7538b |
0.0285 |
0.2987825 |
0.7028103 |
| 0x1bd50e5c36e7112a741bff350975d0859d88776c |
0.0275 |
0.2713236 |
0.6158289 |
| 0xb8b9c9ae6bc6e67d0dc8c3bdd7a7afa3b28be3b8 |
0.0269 |
0.3039554 |
0.674839 |
| 0x93033f52b2cd69040adea284b4e5c4675411a744 |
0.0269 |
0.3039554 |
0.674839 |
| 0x1db0cbd61666cc18b800cd7a540742c6ddf9d41c |
0.0267 |
0.2724794 |
0.6004563 |
| 0xaeaf8371bf9df3edb08bdd7d05099d49965fdf59 |
0.0235 |
0.3042979 |
0.5902068 |
| 0xbda0136ea391e24a938793972726f8763150c7c3 |
0.0235 |
0.3042979 |
0.5902068 |
| 0x707d306714ff28560f32bf9dae973bd33cd851c5 |
0.023 |
0.3042783 |
0.5776145 |
| 0x770bebe5946907cee4dfe004f1648ac435a9d5bb |
0.023 |
0.3042783 |
0.5776145 |
| 0x5917f052f23993680ca51ac7a3453c4566c7013b |
0.0205 |
0.2731805 |
0.4622148 |
| 0x35e6fc00e3f190a8dfe15faa219368a01028ec14 |
0.02 |
0.30429 |
0.5022933 |
| 0x4aef8b6ca98ca20087e6b0827a50868172a32afd |
0.02 |
0.30429 |
0.5022933 |
| 0x76ac6ad4e4e7c2e0b4ceeb30745bd53df3a85774 |
0.02 |
0.30429 |
0.5022933 |
| 0x91ebba819e4bba03065a106290afcb44deb1f9d6 |
0.02 |
0.225295 |
0.3718913 |
| 0x41145a1132655d145458e73da80a43070eea68da |
0.018 |
0.3044611 |
0.4523133 |
| 0xefb823e3b4481f3c5526370c7d9e009040c0028a |
0.0149 |
0.3060671 |
0.376392 |
| 0x3f44e4b482295bafa71f6faf4131ec7007f63e29 |
0.0149 |
0.2229799 |
0.2742167 |
| 0x9d4afb91930fef1c42ed11841a579e5343aca78e |
0.0149 |
0.3084295 |
0.3792967 |
| 0xf9d936a03f77397d108d06cedab2f91111559013 |
0.0148 |
0.3093919 |
0.3779305 |
| 0x00432772ed25d4eb3c6eb26dc461239b35cf8760 |
0.0145 |
0.3042828 |
0.3641507 |
| 0x4680349ef7f6b7ce243ac29a680bcd02444e17cc |
0.0138 |
0.3083768 |
0.3512328 |
| 0x1b5b4fcedf1252cd92496a2fd5c593b39ac49b01 |
0.0124 |
0.3042823 |
0.3114128 |
| 0xb61712f928927cc88b05e376579e0bc76c5b6b06 |
0.012 |
0.3089417 |
0.3059801 |
| 0x7a3bdee62dd34fac317ae61cd8b3ba7c27ada145 |
0.0112 |
0.3043125 |
0.2813029 |
| 0xa4d506434445bb7303ea34a07bc38484cdc64a95 |
0.0082 |
0.2802317 |
0.1896611 |
| 0xe7a07da6c5c37ae70067ce9374a53a6288105bf3 |
0.0071 |
0.3087887 |
0.1809502 |
 GovWatch
GovWatch
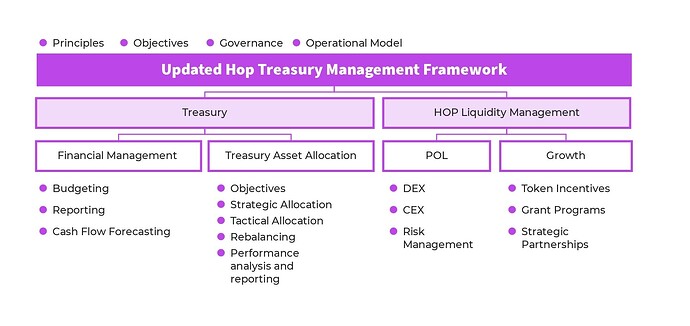
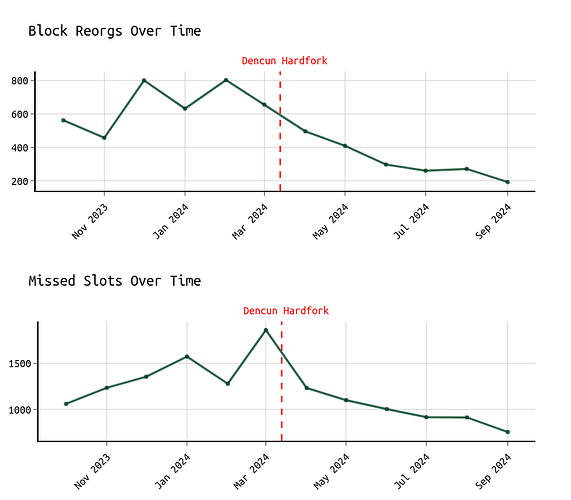
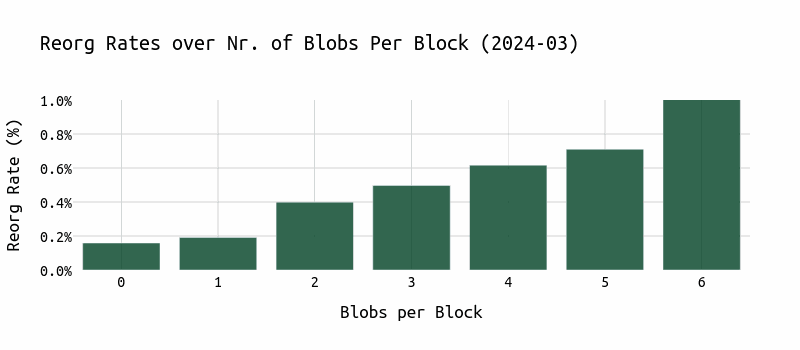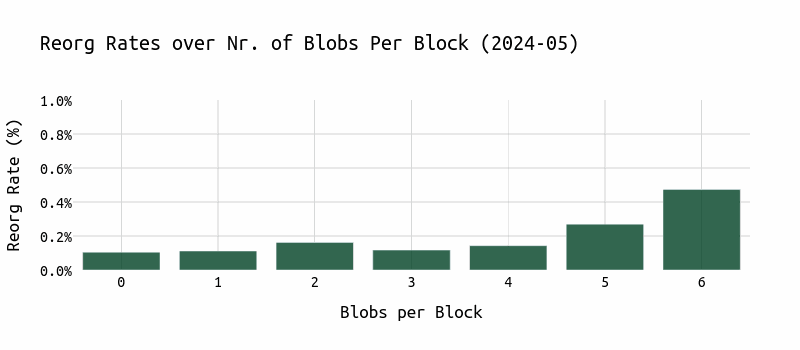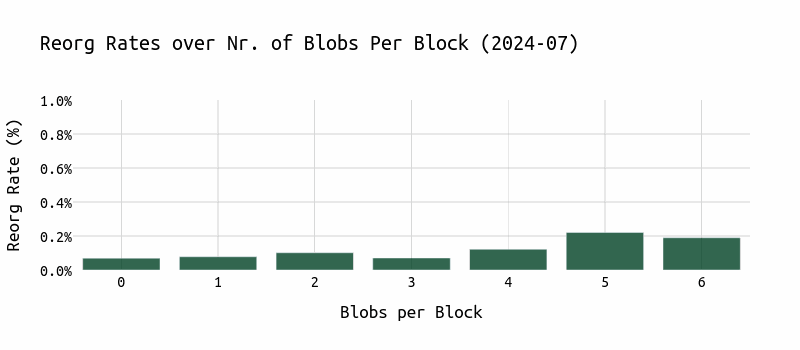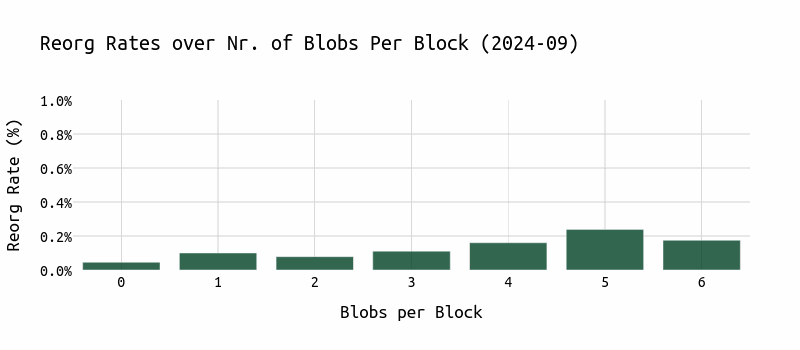
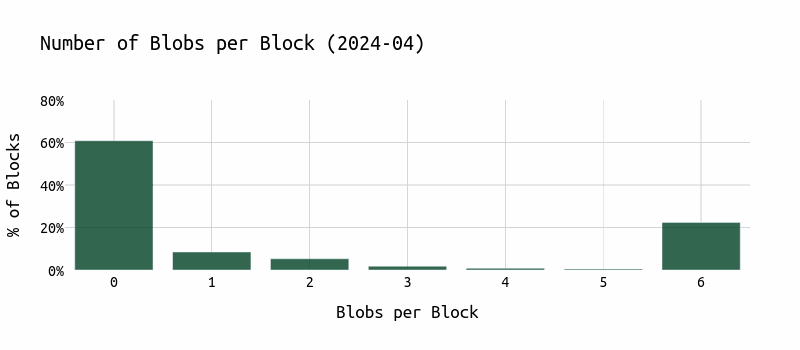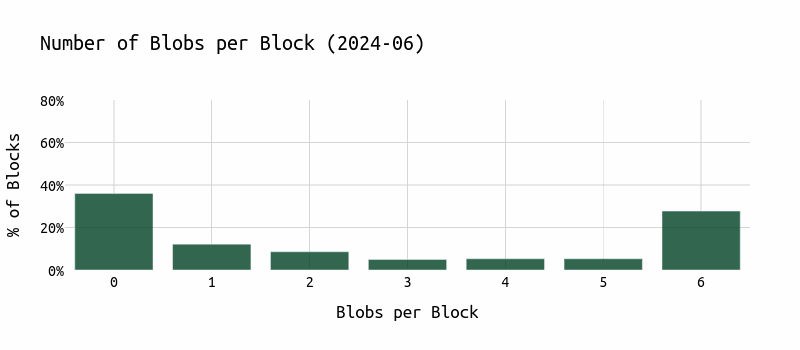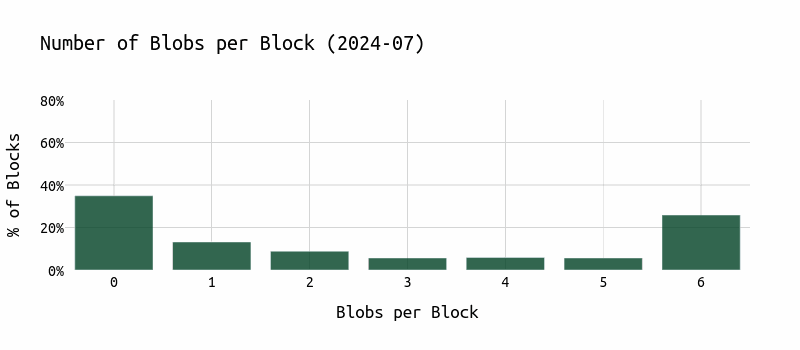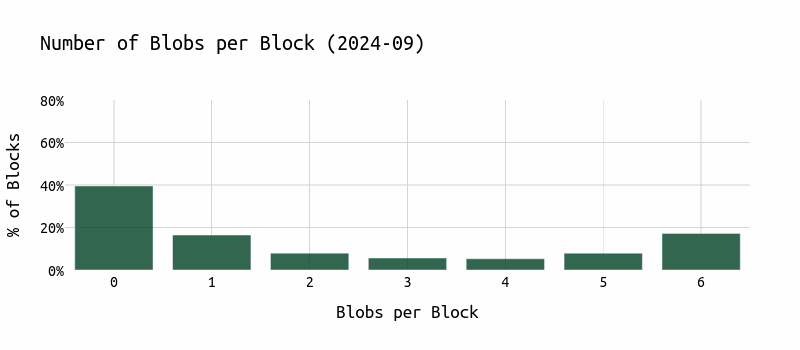

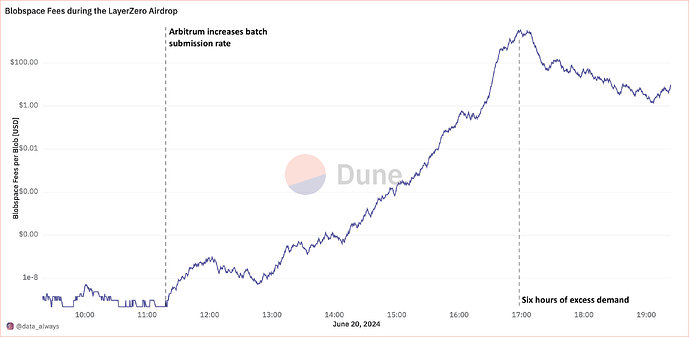
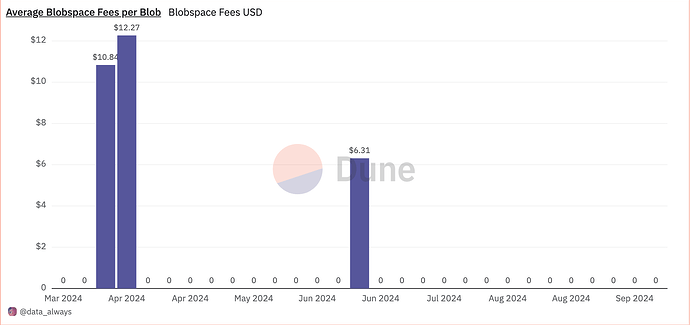
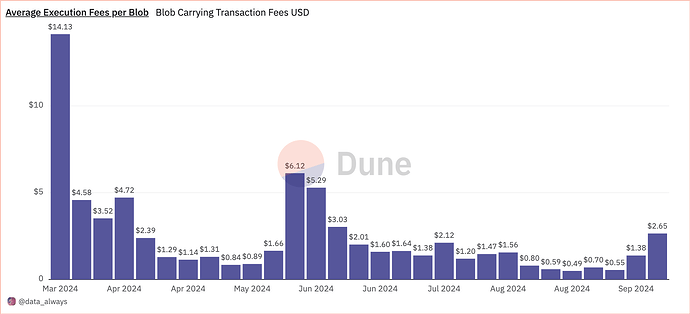
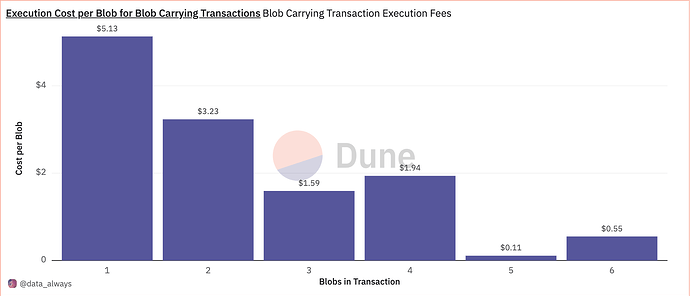
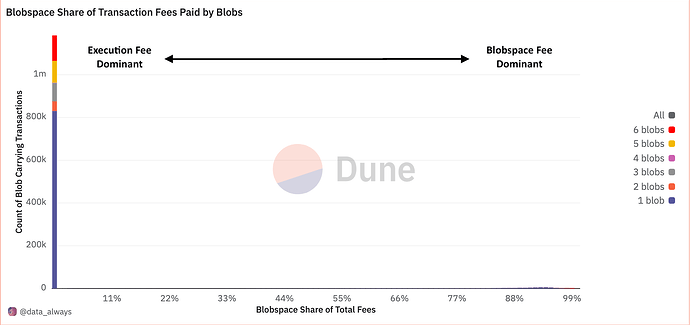
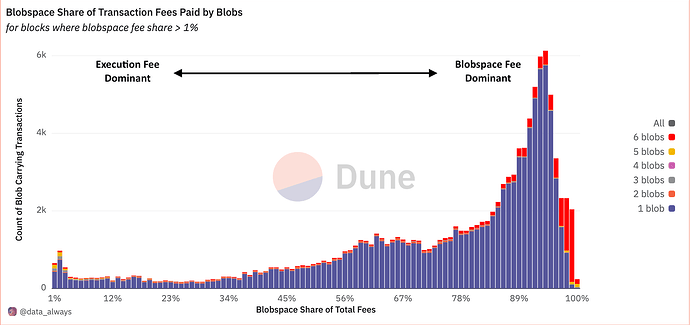
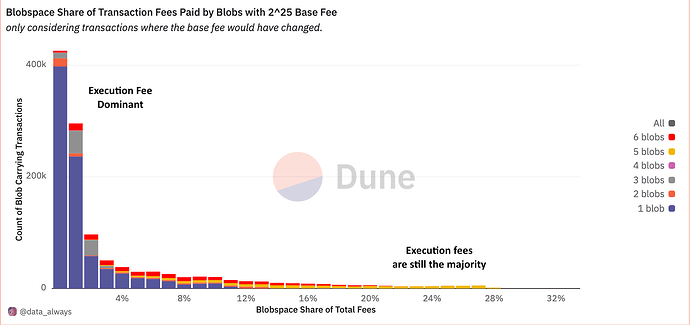
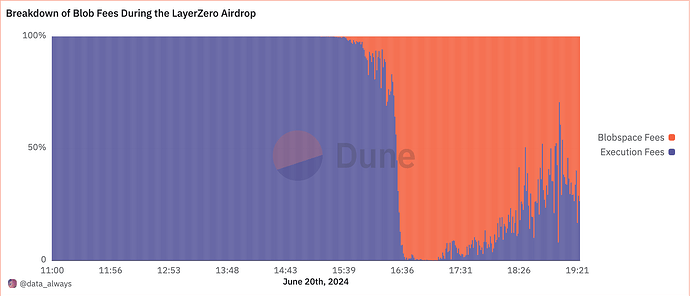
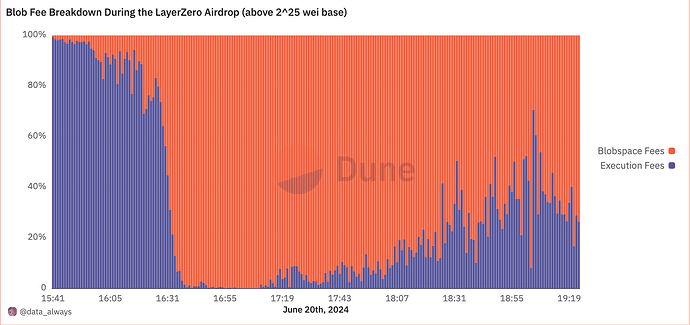

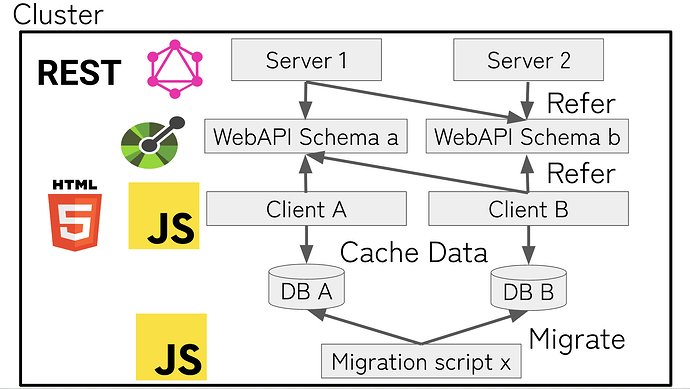
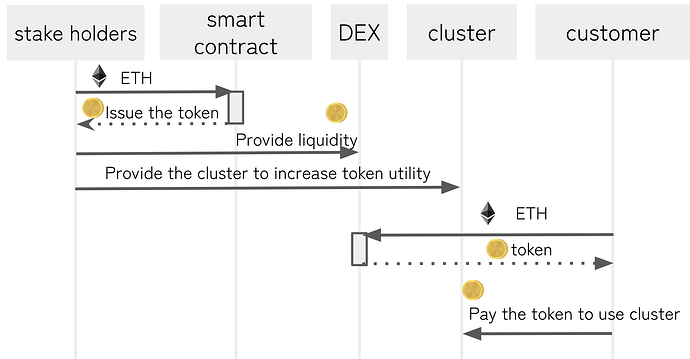
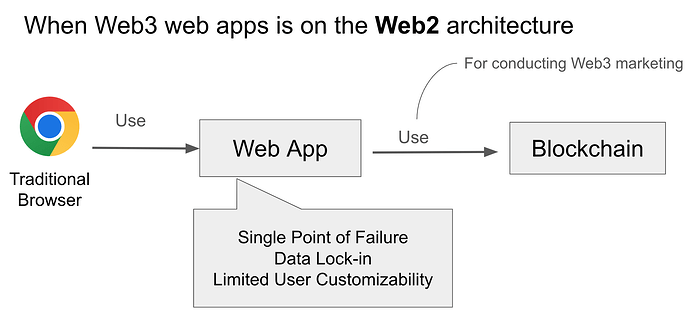
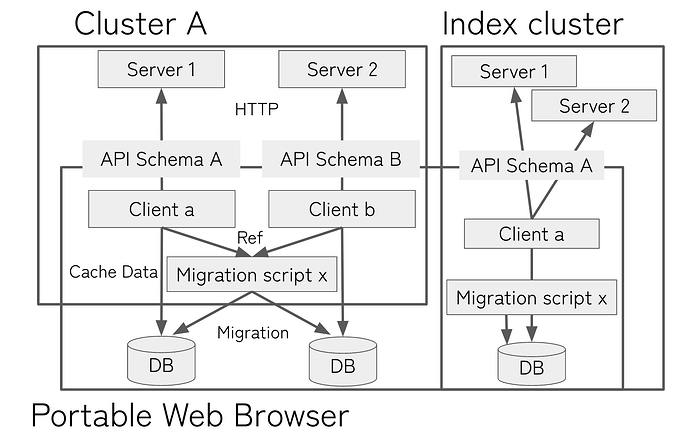
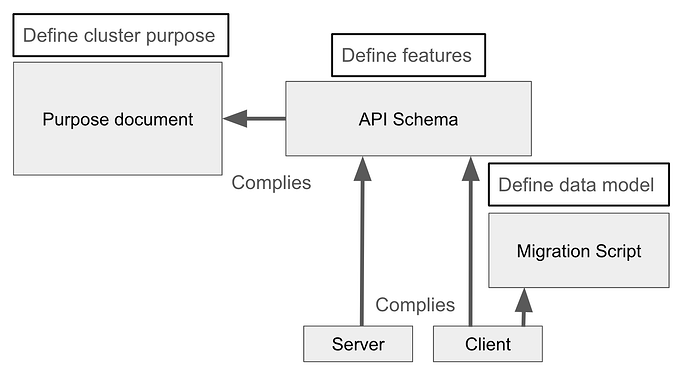
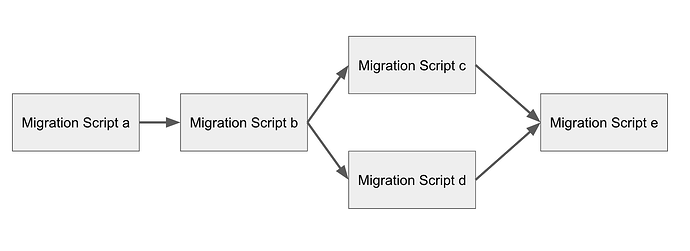
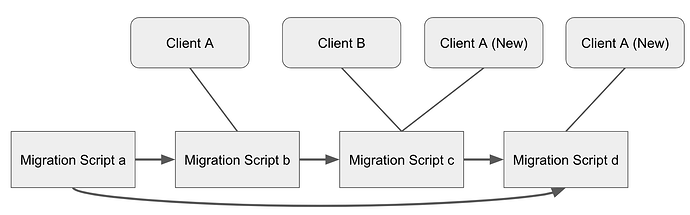
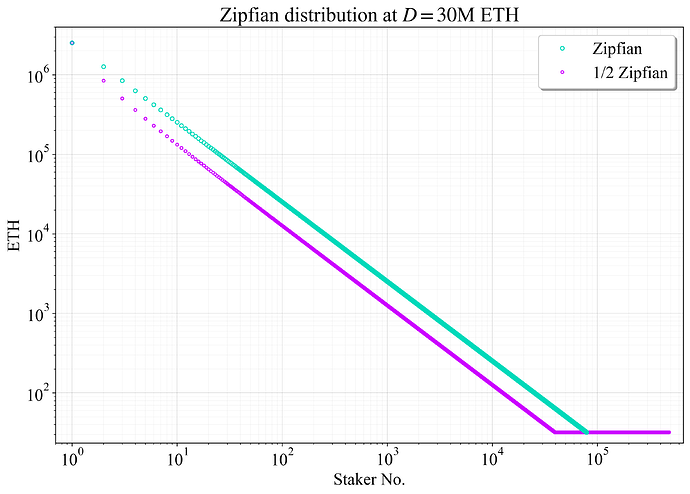
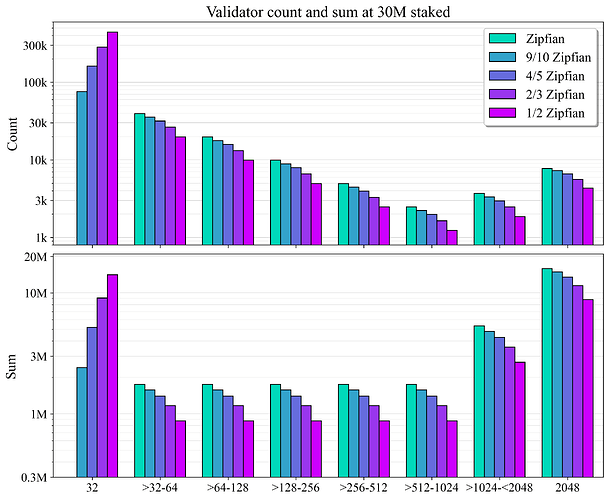
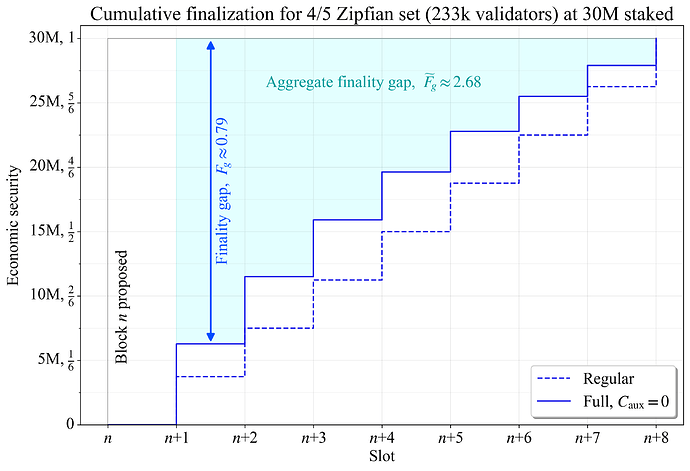
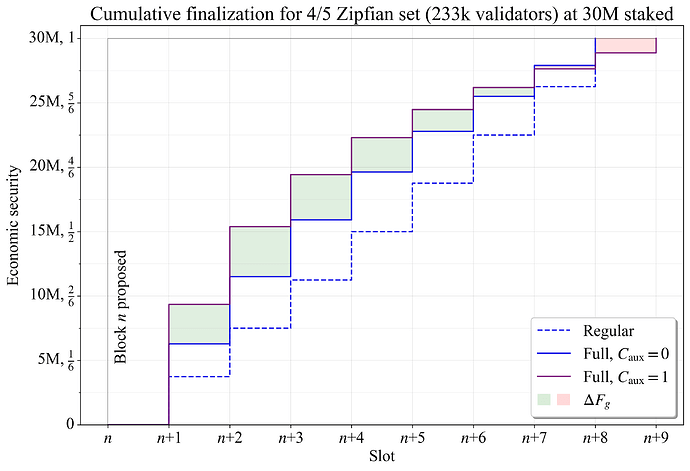
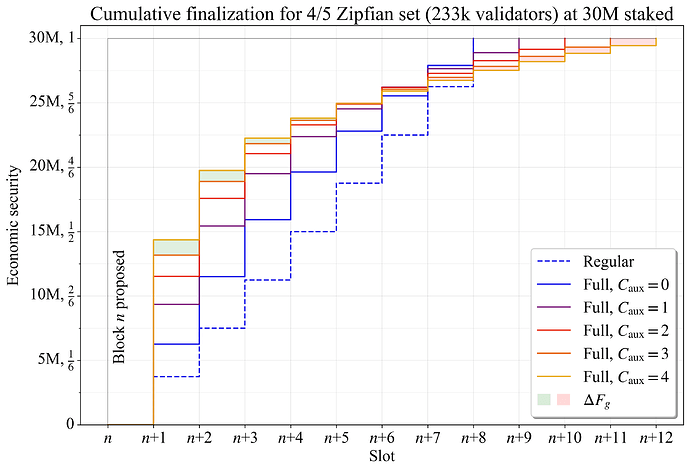
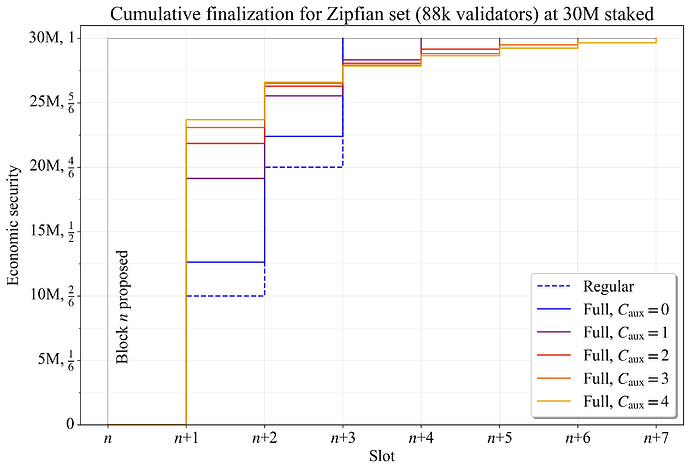
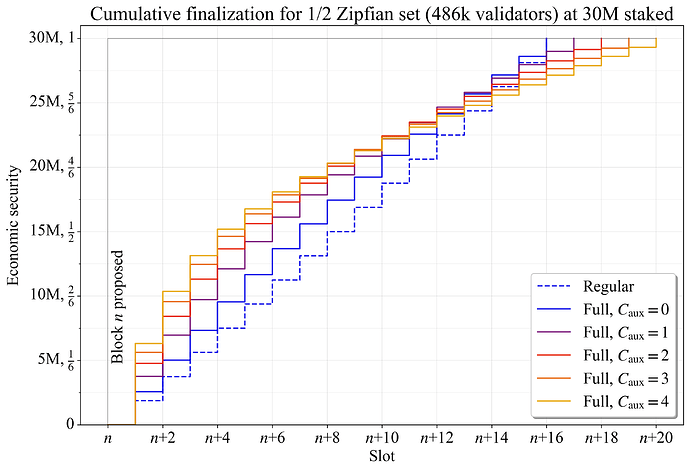
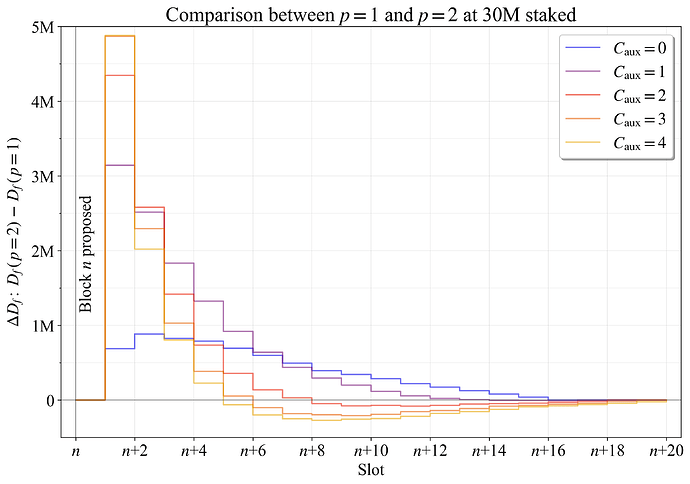
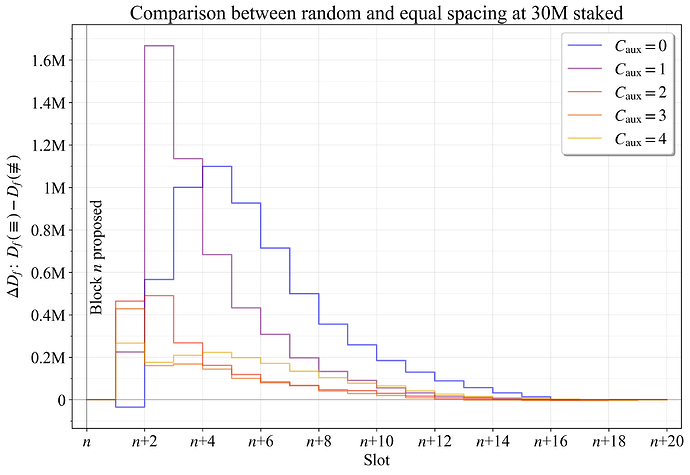
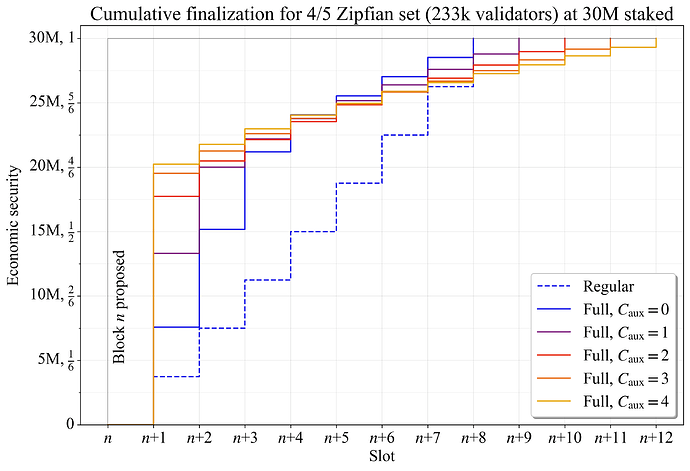
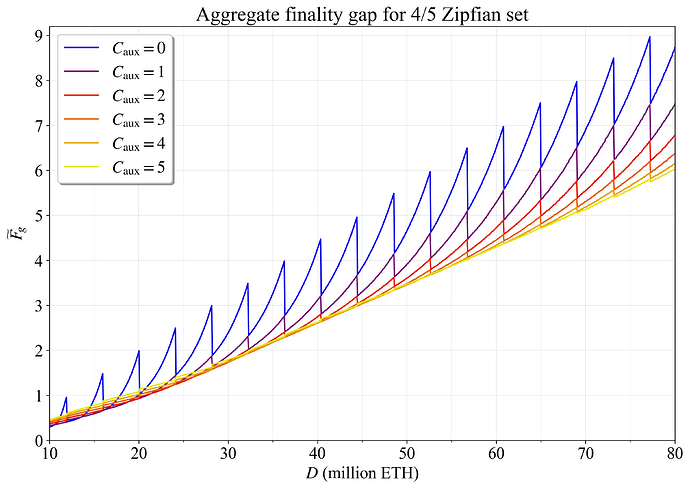
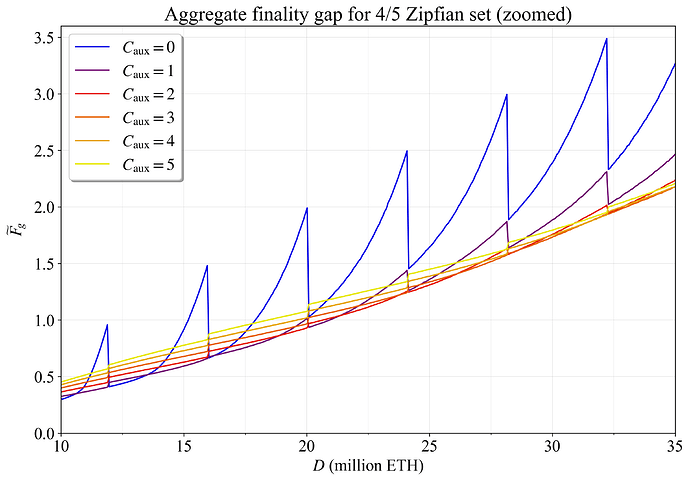
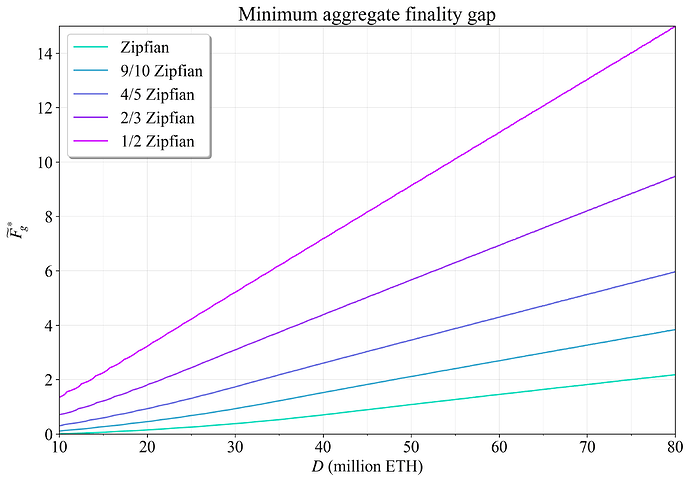
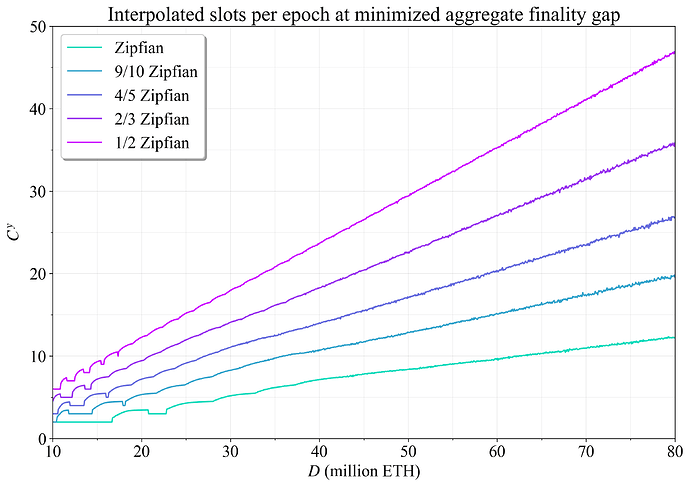
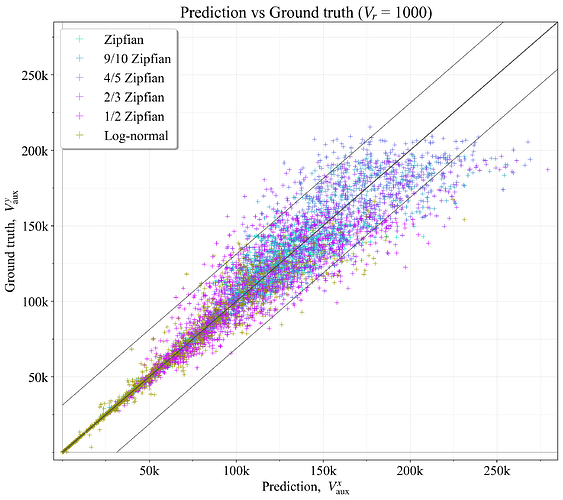
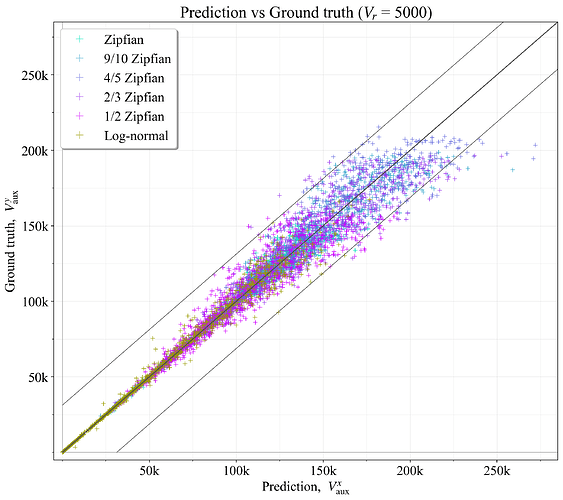
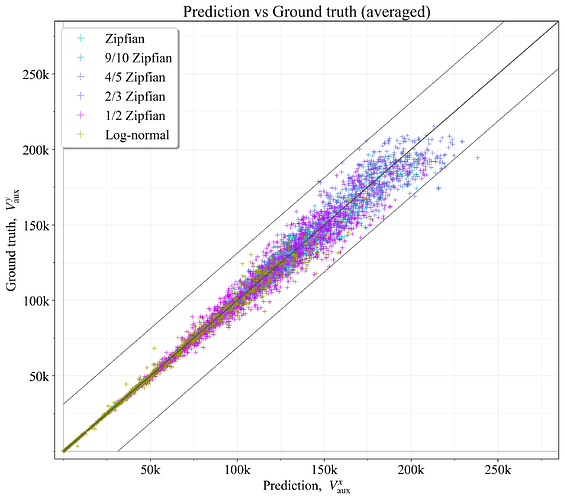
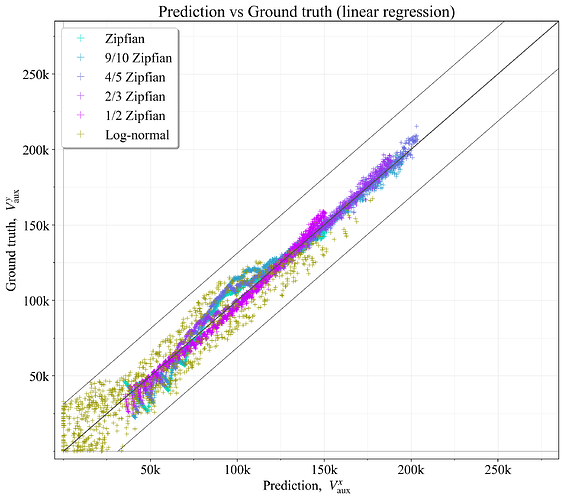
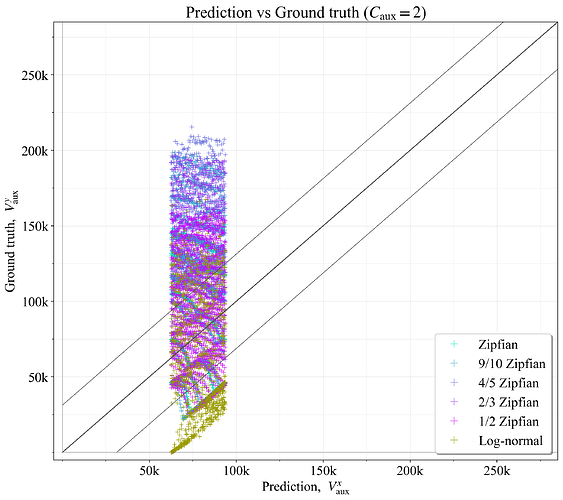
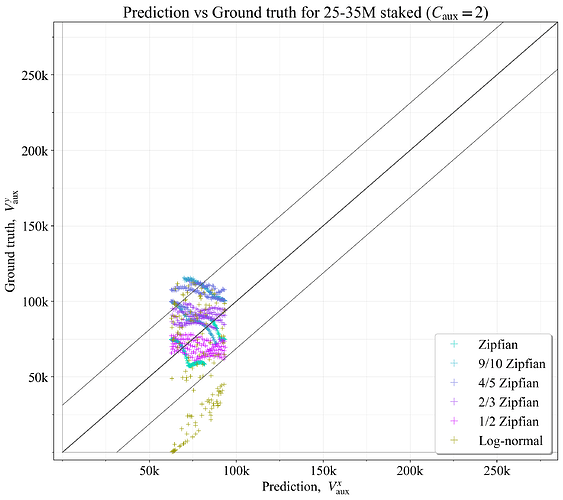
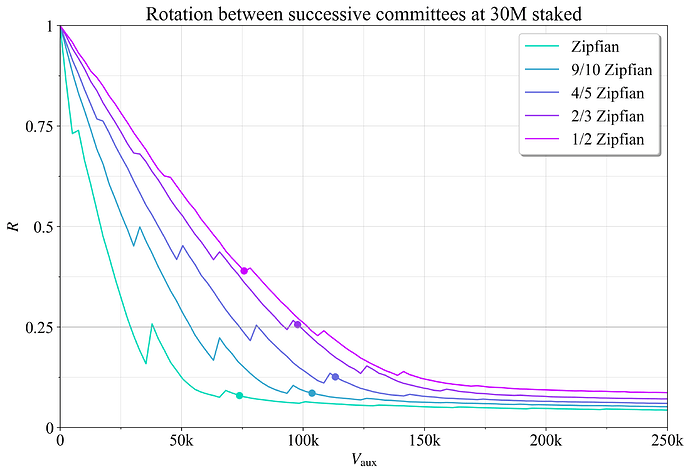
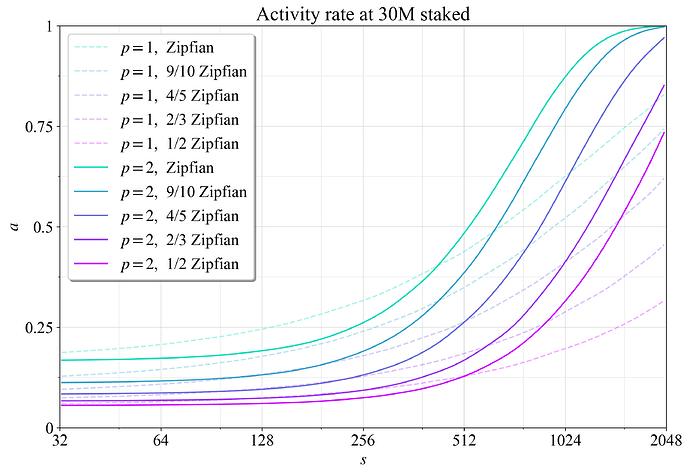
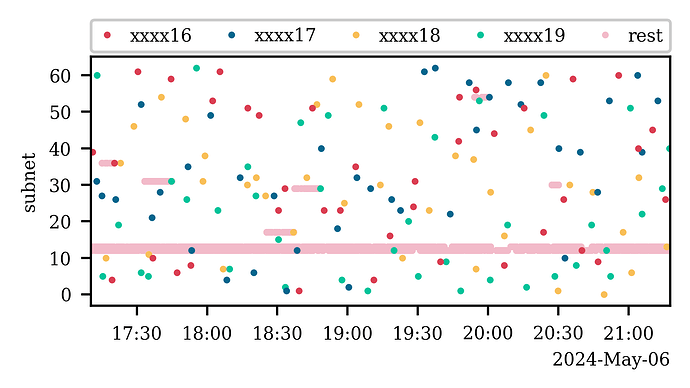
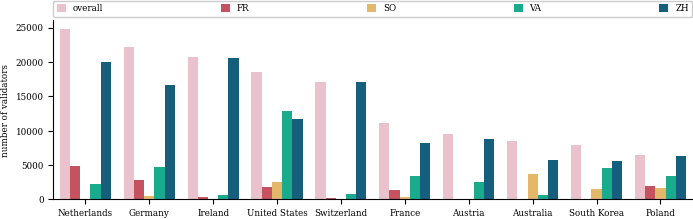
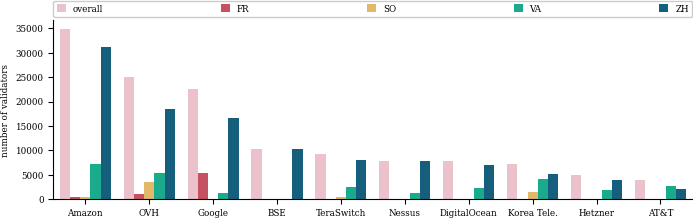
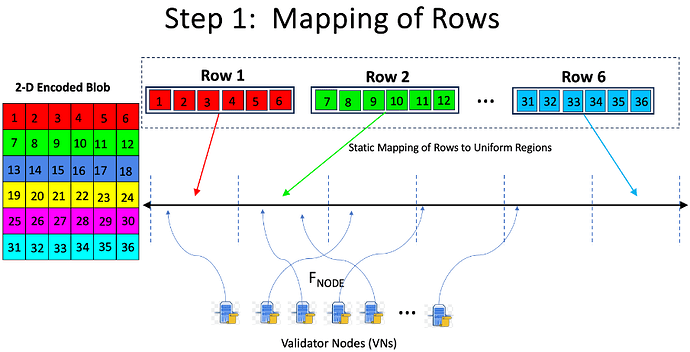
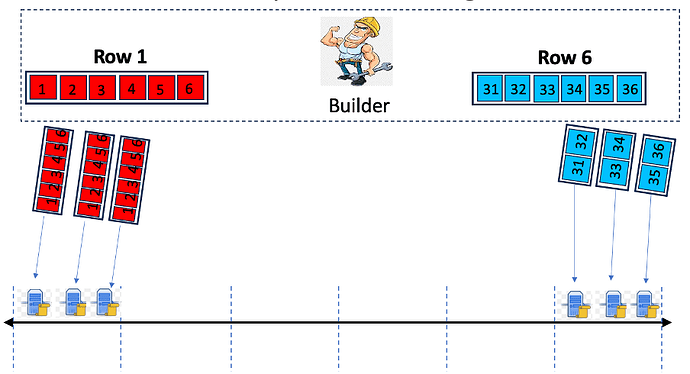
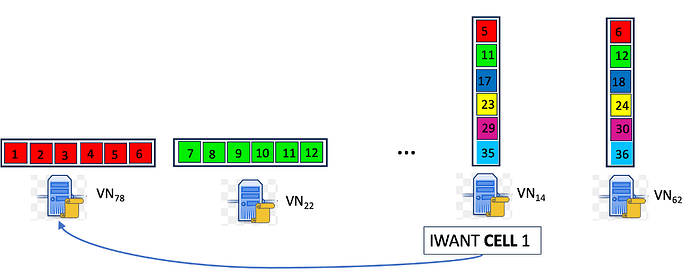
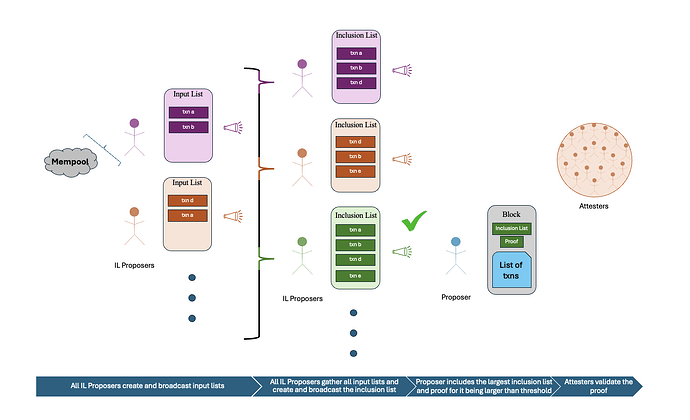
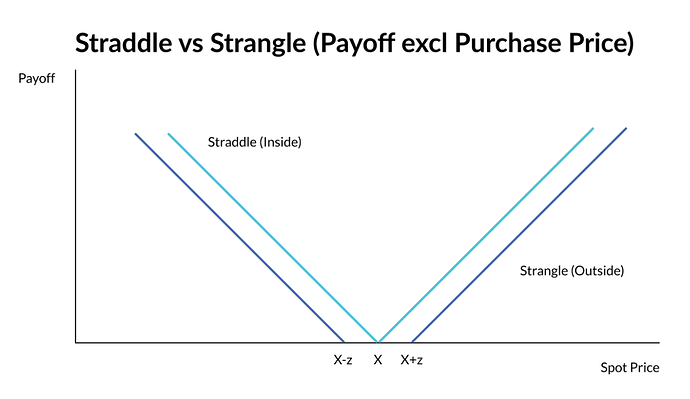
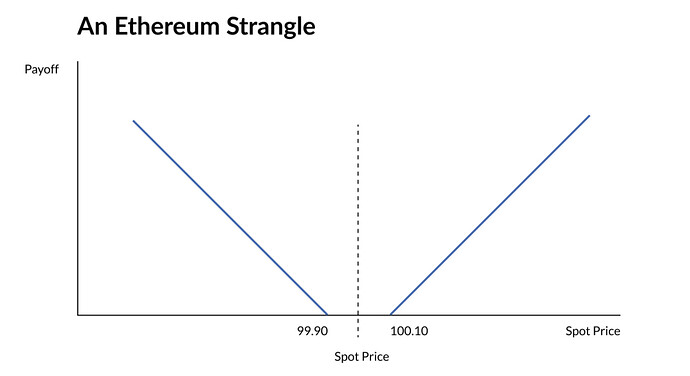
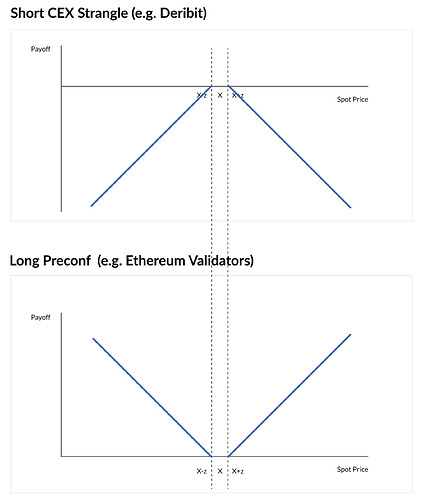
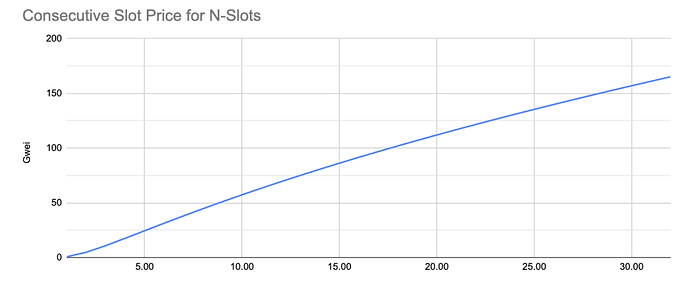
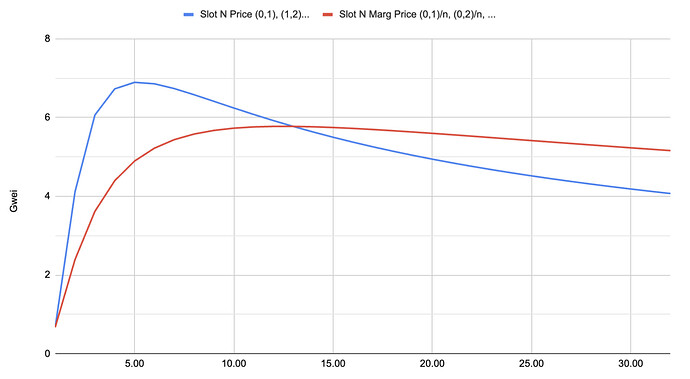
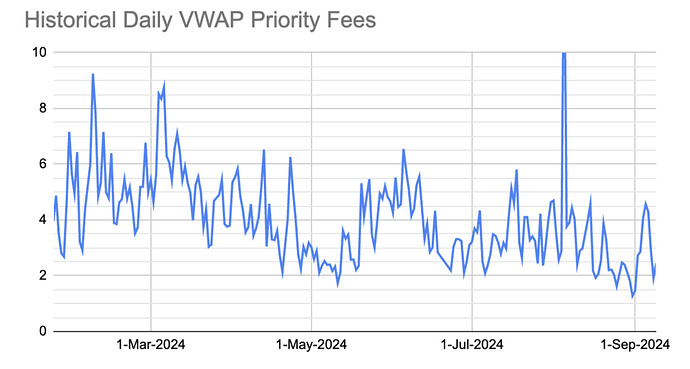
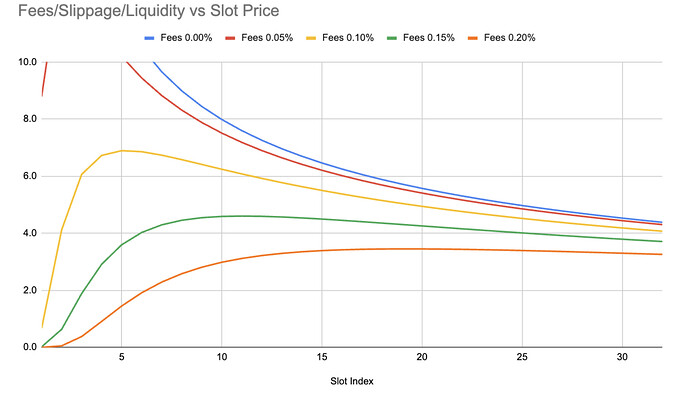
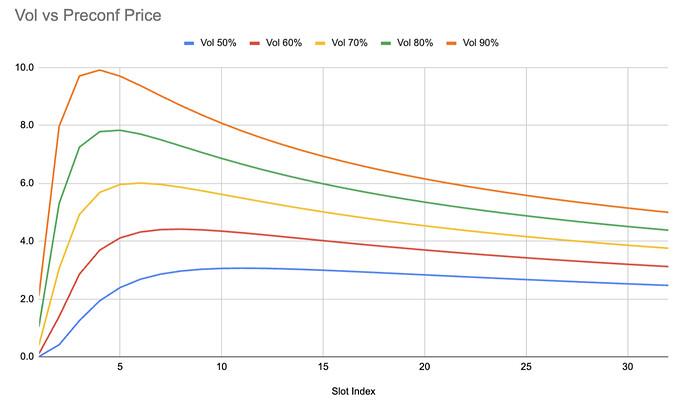
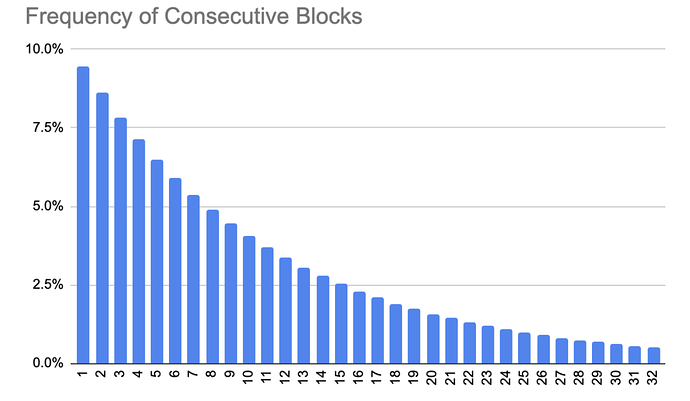
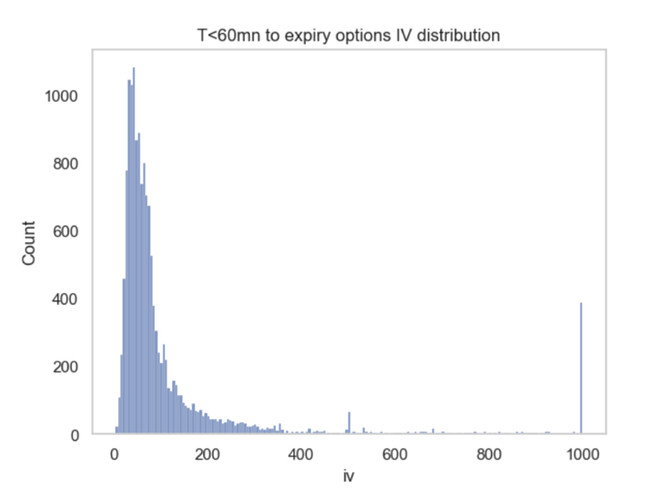
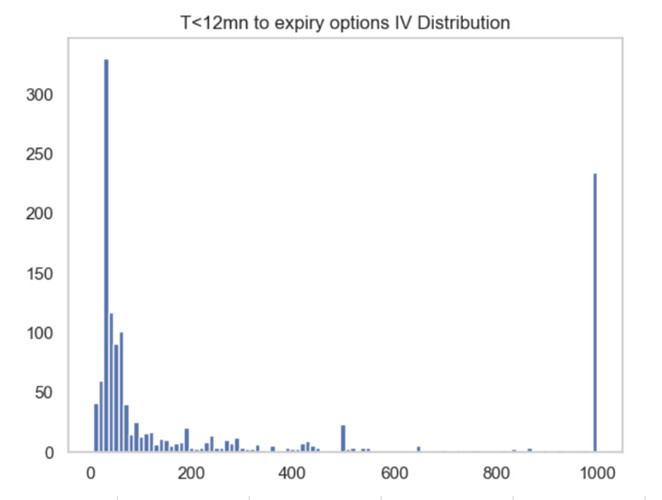
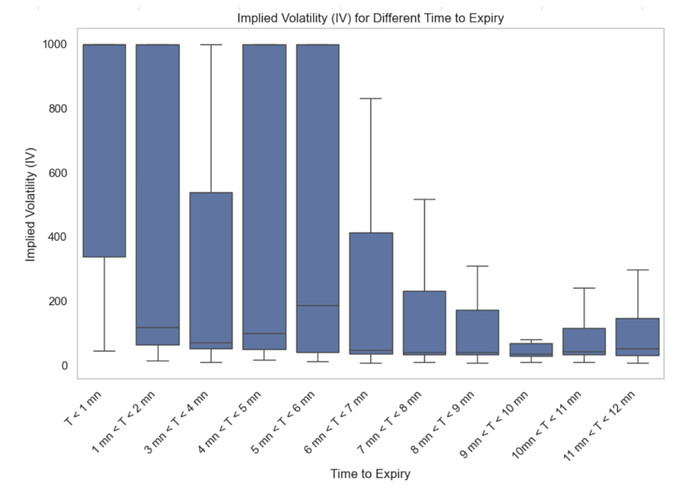
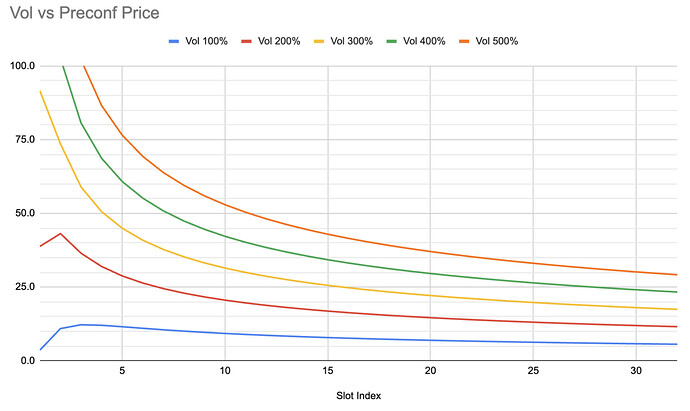
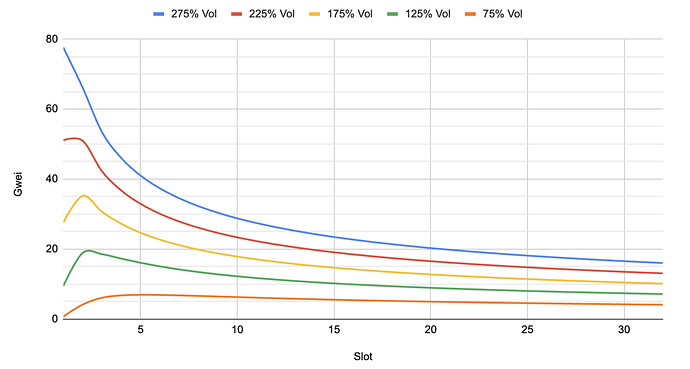
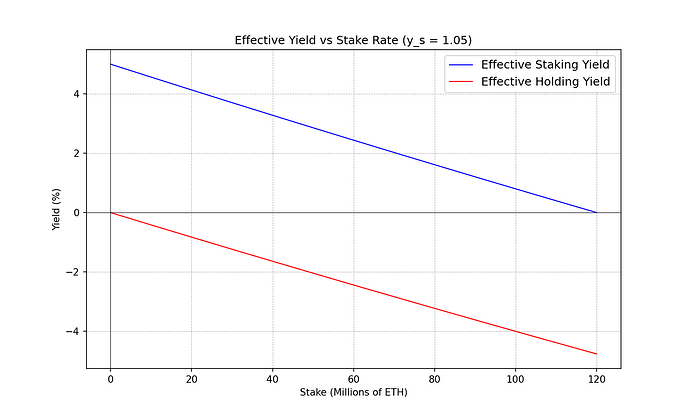
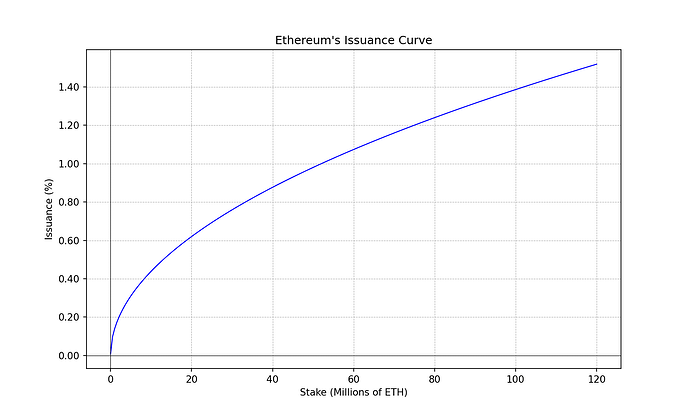
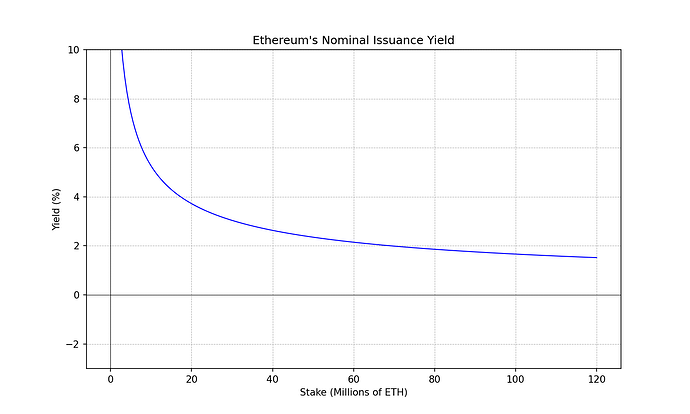
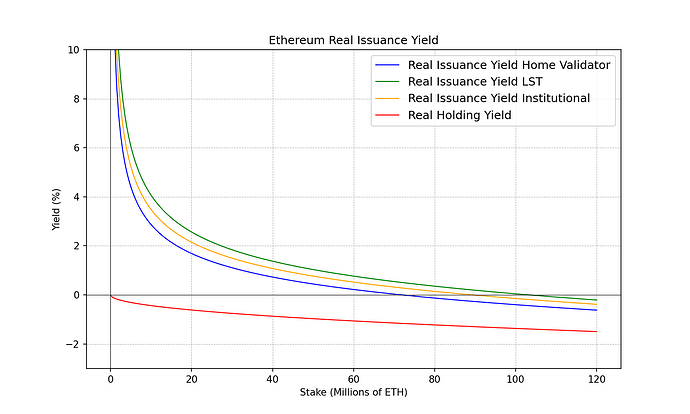
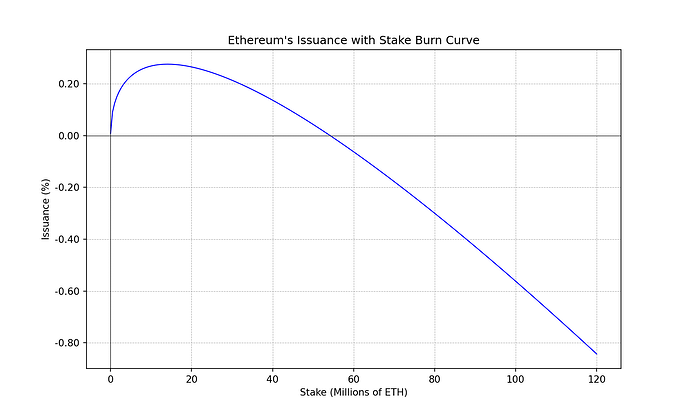
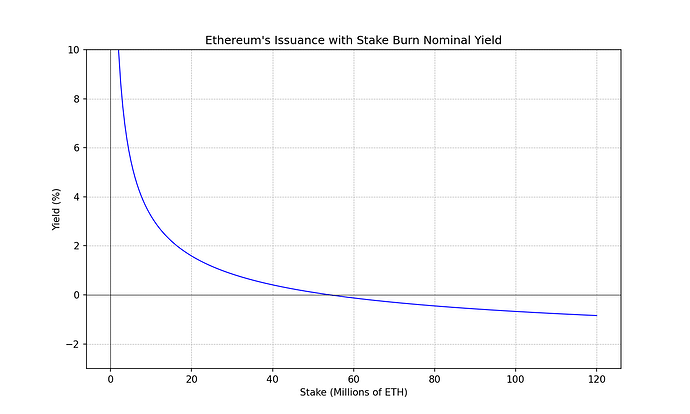
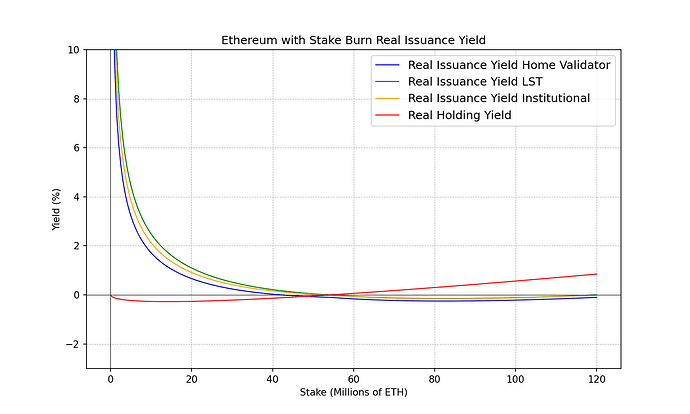
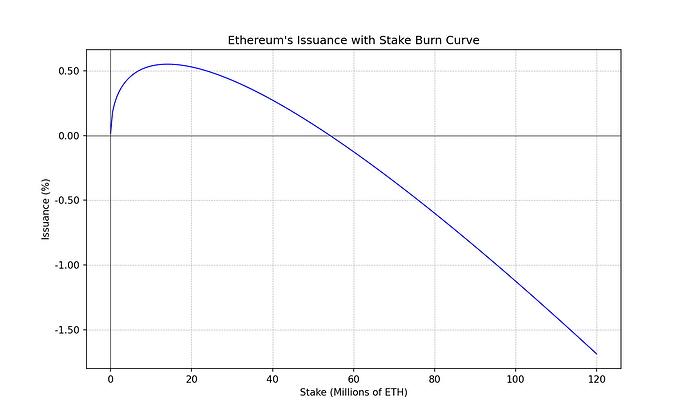
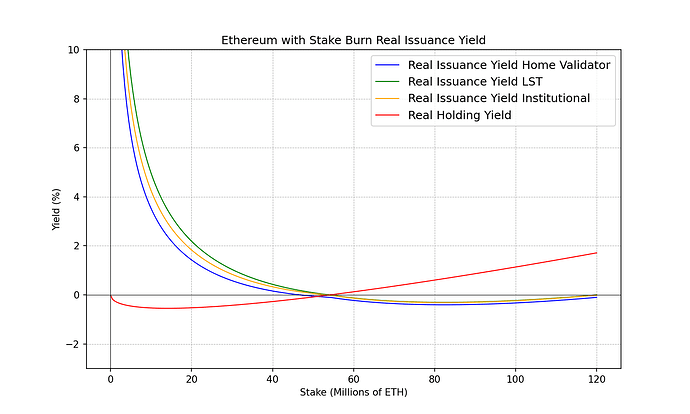
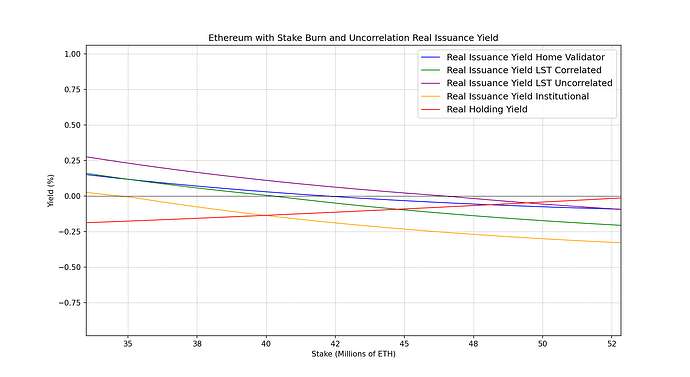
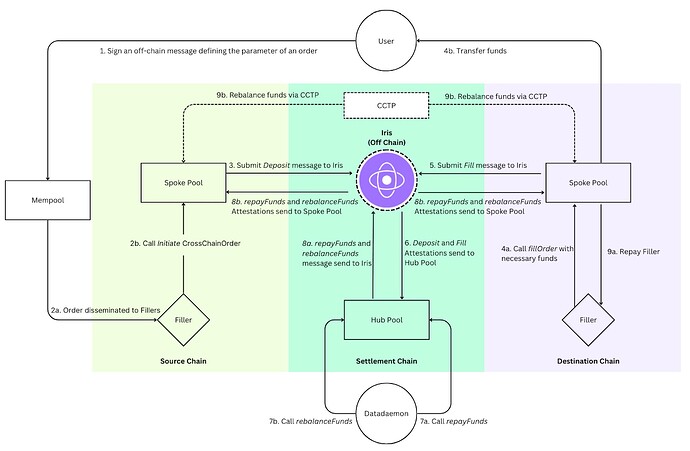
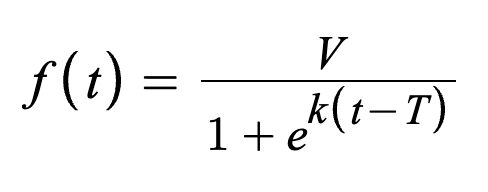
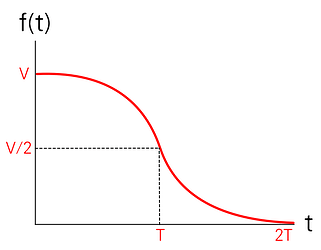
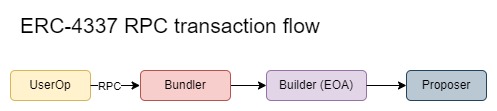
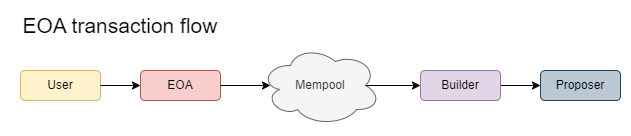
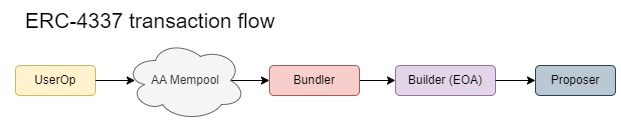
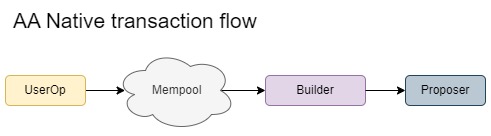
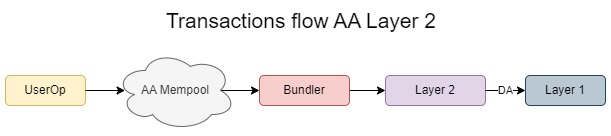
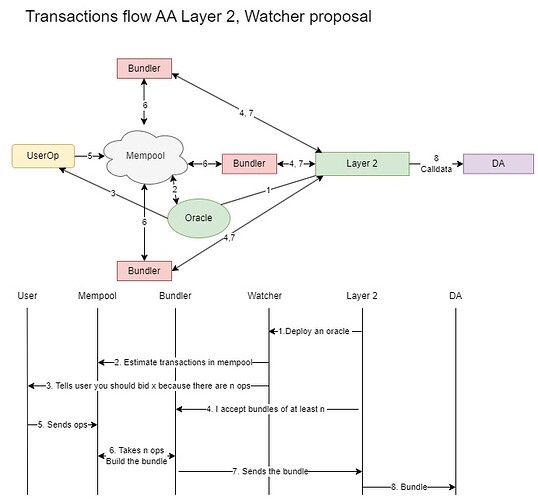
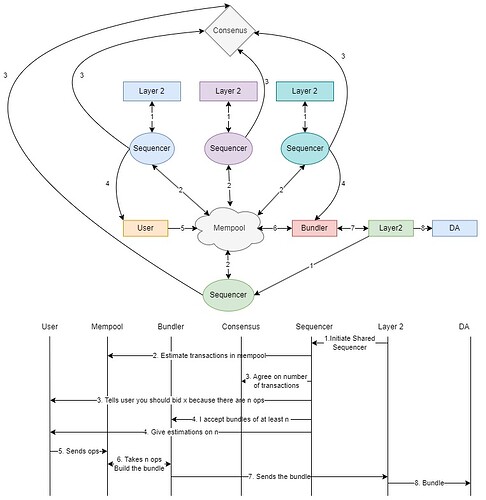
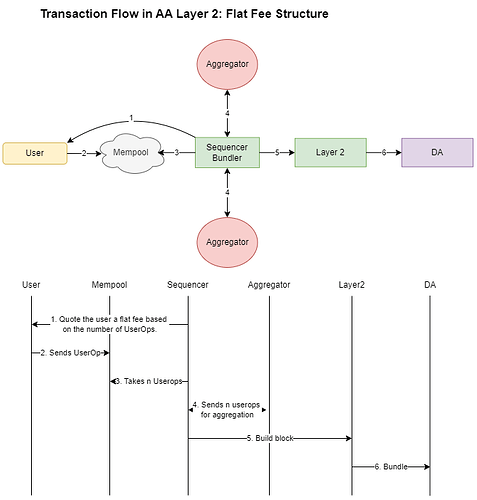
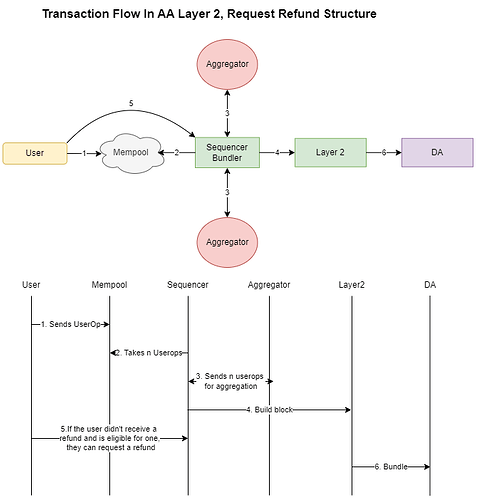
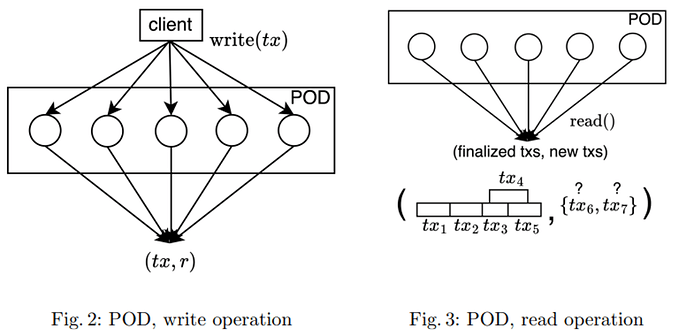
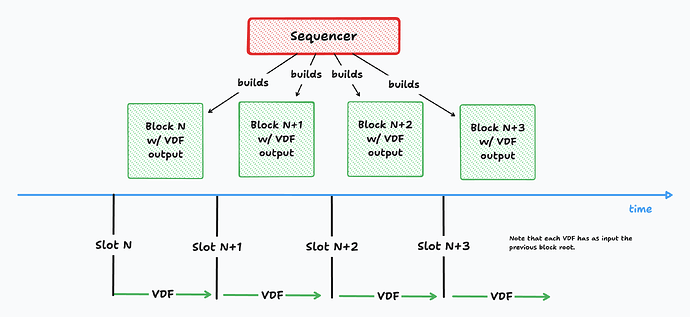


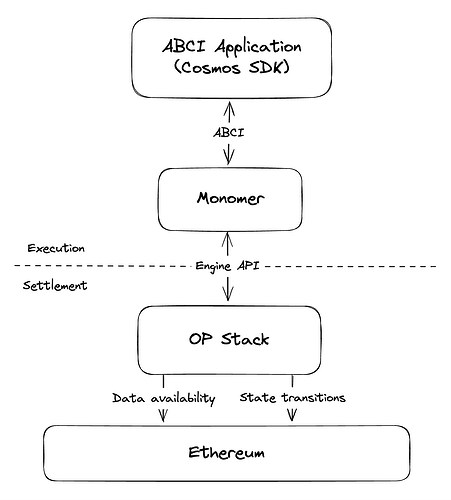
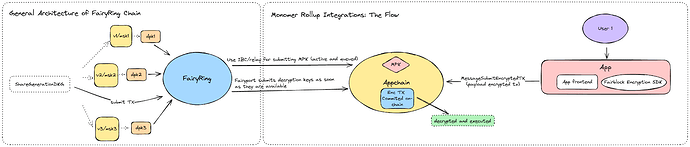
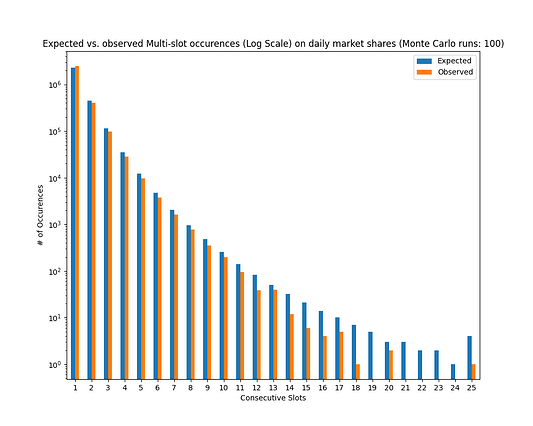
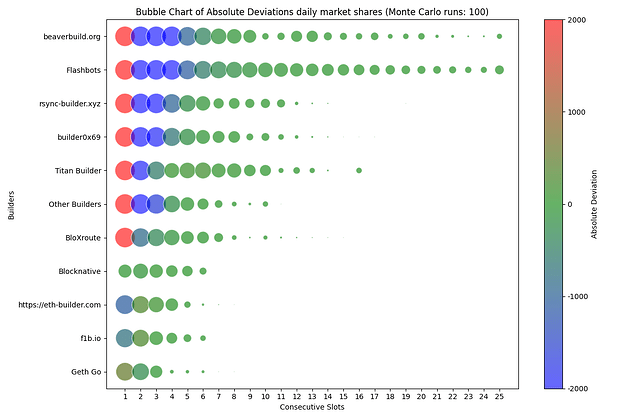
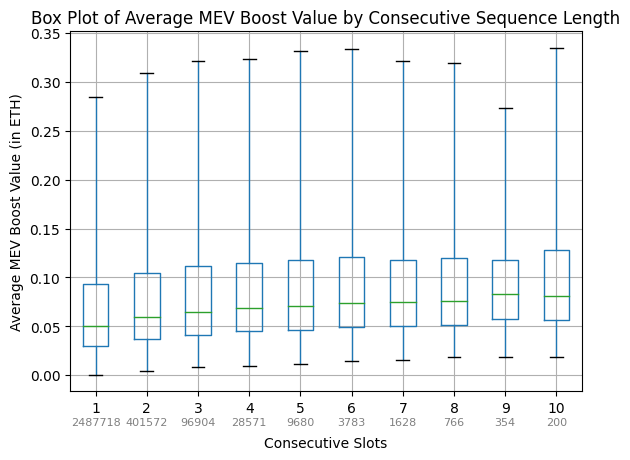
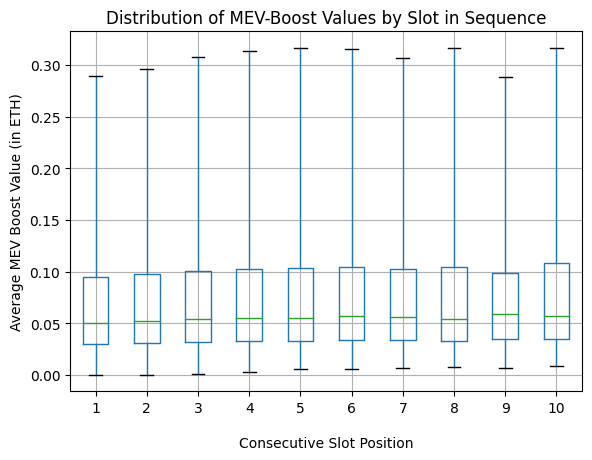
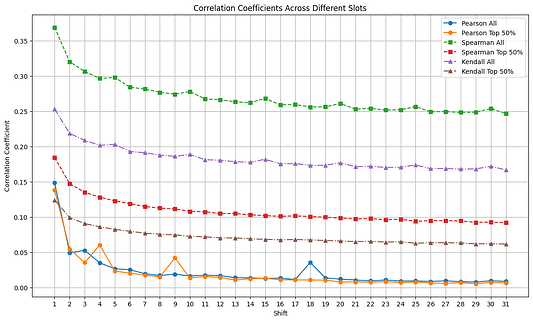


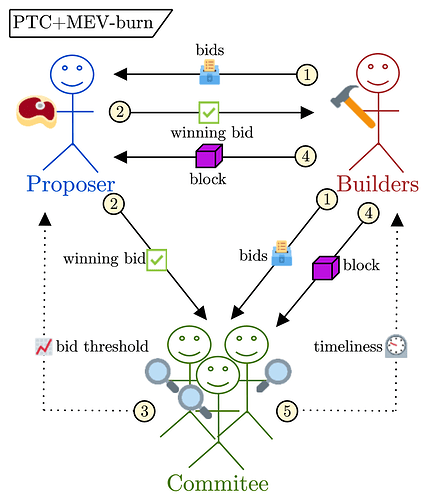
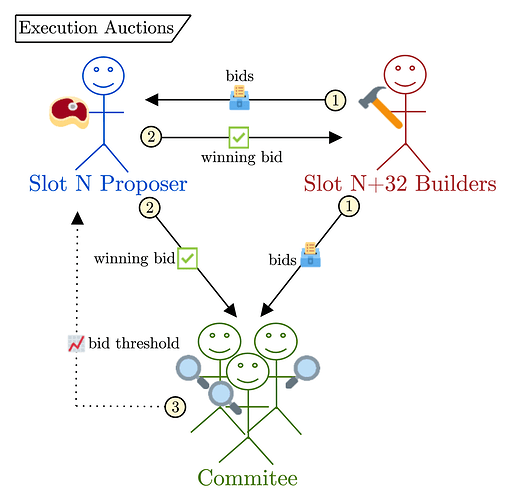
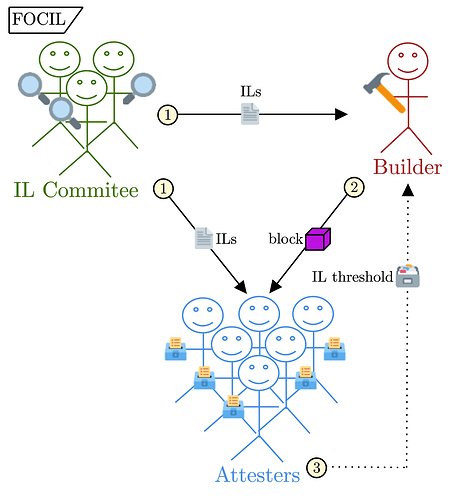

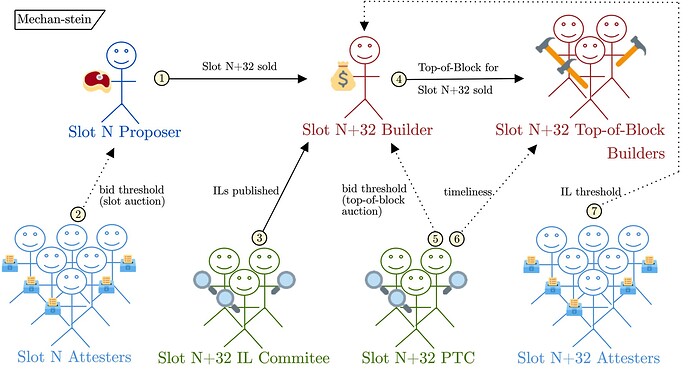
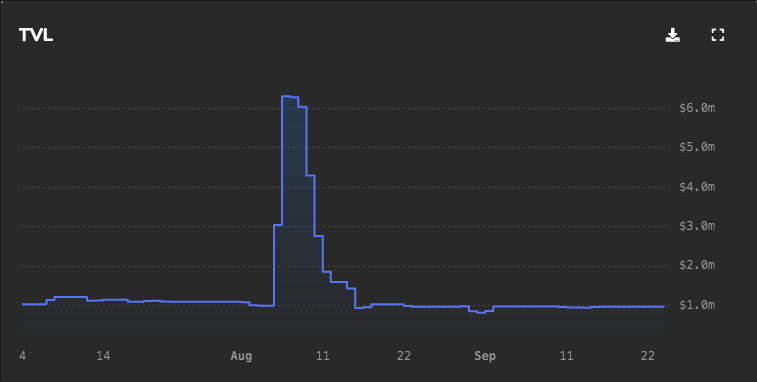
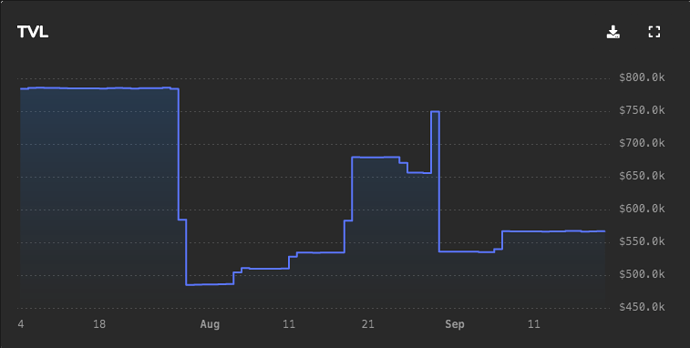

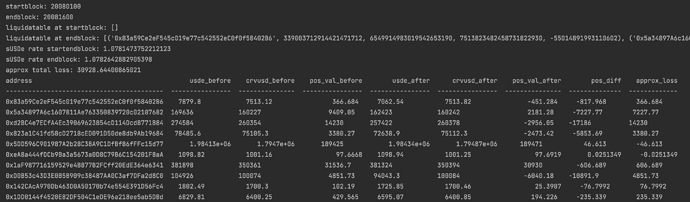
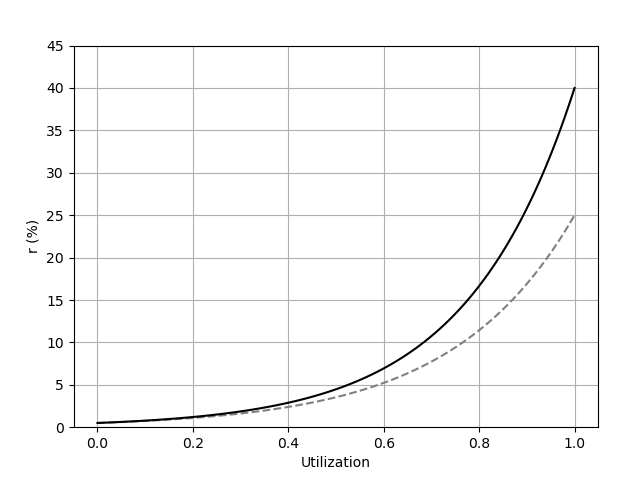
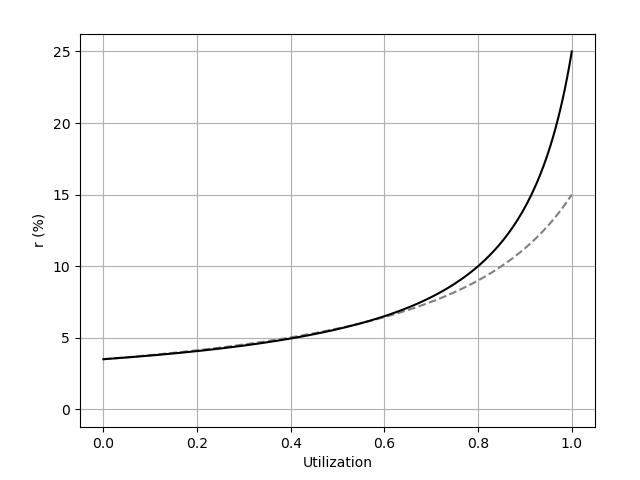
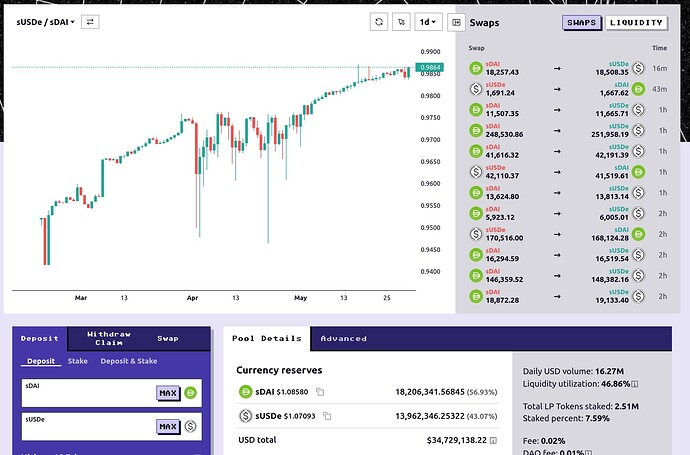
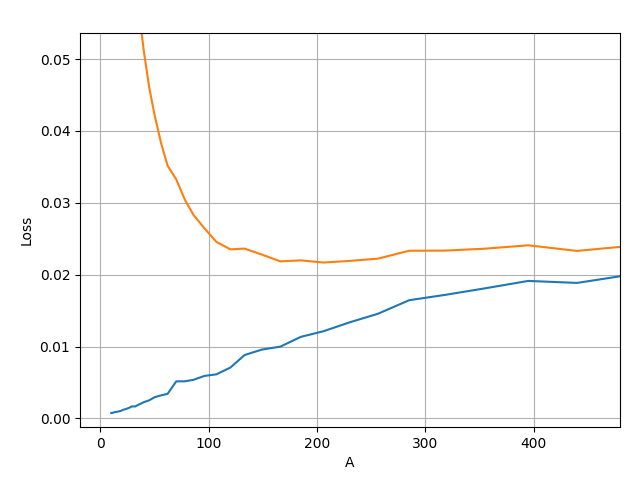
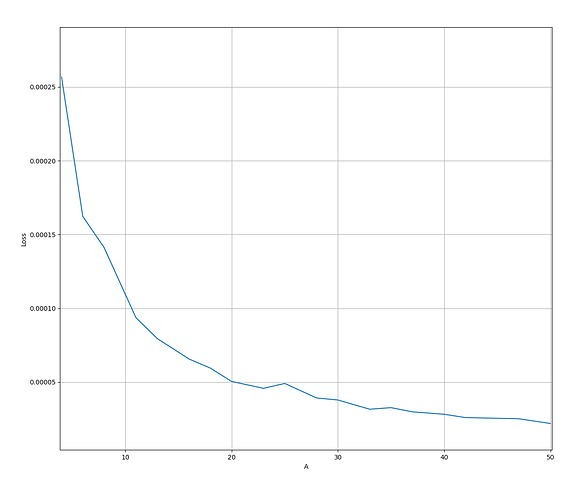
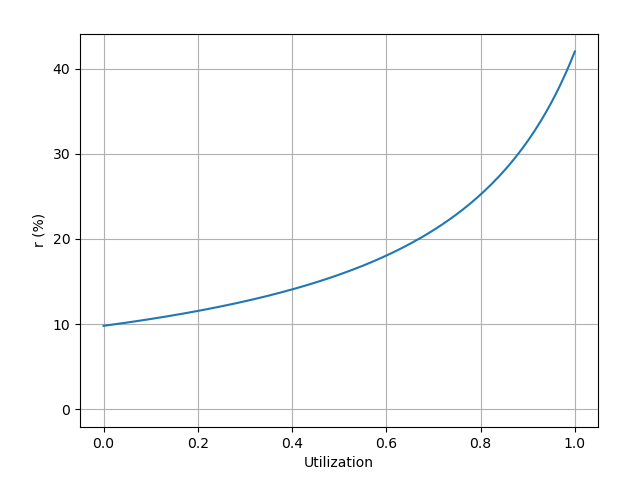
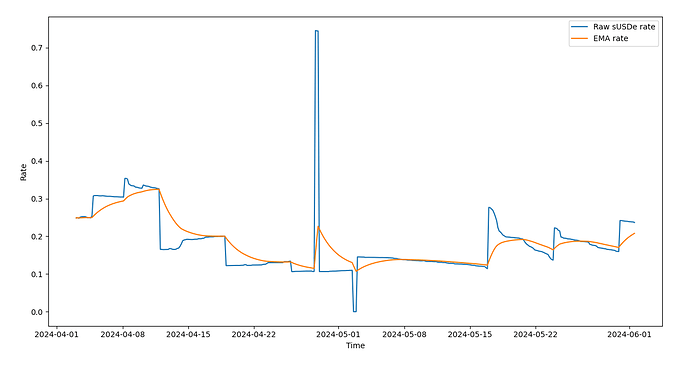
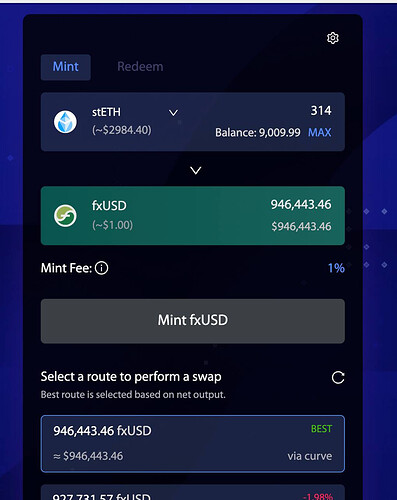
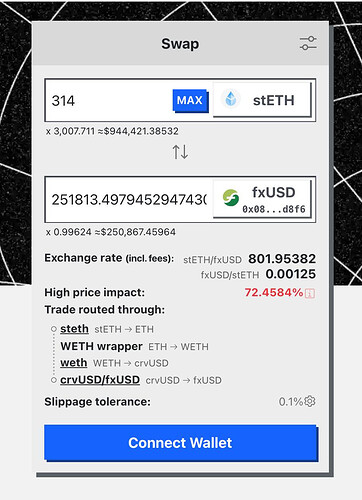
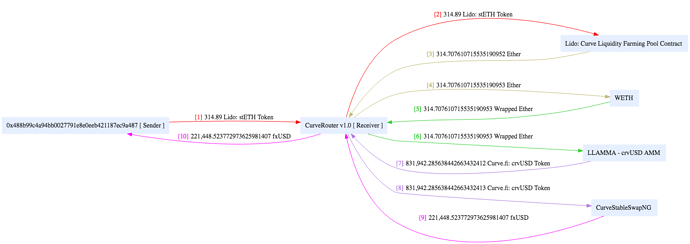
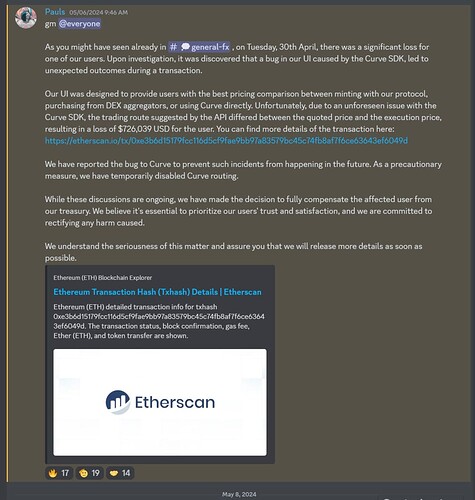















































































































































































































































































































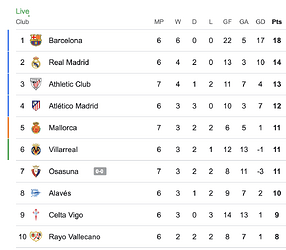
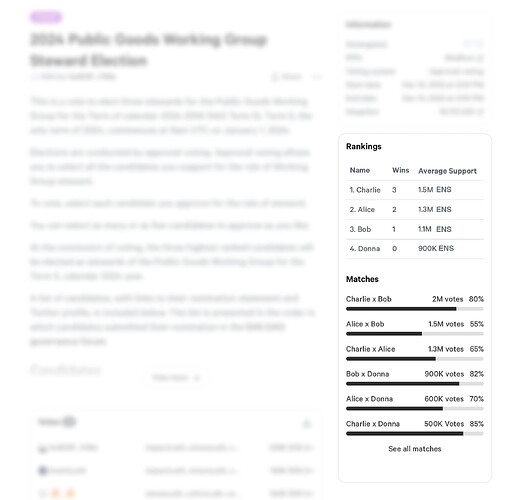

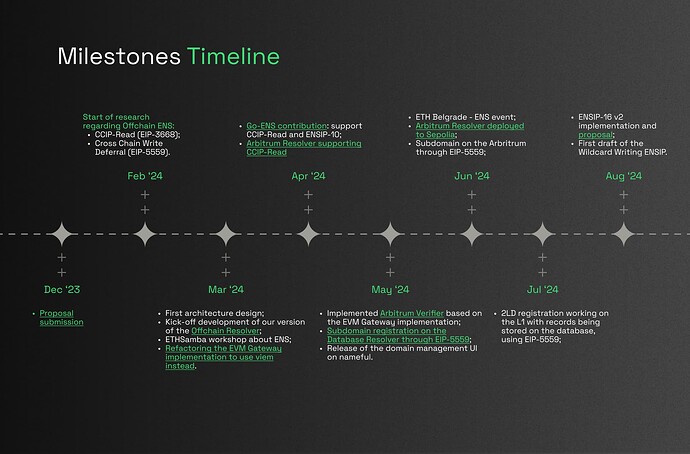
![L2 subdomain registering [WIP]](https://discuss.ens.domains/uploads/db9688/optimized/2X/c/cdc3bd31677396be7ae4b3d1d26b4e98b2f3cb4b_2_690x332.png)